1．已知A={第一象限角}，B={锐角}，C={小于90°的角}，那么A、B、C关系是(　　 )

6．已知函数f(x)＝x+三，且f(1)＝2．(1)求m；　 (2)判断f(x)的奇偶性；

　(3)函数f(x)在(1，+∞)上是增函数还是减函数?并证明．

一1 B；2 C　 3 D ；4 　；5 ；6 ；7　 ， ；8 {9，10，11}　 ；9 为点(4，7)。

　10 ；11　 {－3，2}；12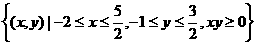

二1B；2B ；3D；4C ；5，－1≤M≤；6，a＞5或d≤－5 ；7，，－ ；8，，{0}，{2}，{0，2}；

9，q＝－；10(1)a＝0，x＝－或a＝1，x＝－1；(2)a≥1或a＝0．

三1D；2A；3C ；4C；5{y｜－3≤y≤3}；6，4；7，－1，0，±；8，a的值为0，，－1．9，25人．

四1D ；2；B；3D；4C；5， 3+，57；6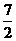，；7(1)(－1，1)∪(1，2)；(2)R；(3)(－∞，0)．8，(1)(－∞，)；(2)［－15，7］；(3)［－4，0］；(4)(－4，+∞)．

五1A ；2D ；3B ；5，18，4或－，；5，V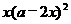＝，{x｜0＜x＜a/2}；6，(，－)；

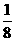7　　 8

六1C ；2A；3，(－∞，－1)，(－1，+∞)；4，［0，］，(－∞，－)；5，增区间(1，+∞)，减区间(0，1)；6，3小时；7，x＞3或x＜－1． 七1D；2B ；3A ；4，－26 ；5，f(a²一a+1)≤f()

6解：(1)f(1)：1+m＝2，m＝1．

(2)f(x)＝x+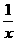，f(－x)＝－x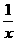－＝－f(x)，∴f(x)是奇函数．

(3)设x₁、x₂是(1，+∞)上的任意两个实数，且x₁＜x₂，则f(x₁)－f(x₂)＝x₁+－(x₂+)＝x₁－x₂+(－)　＝x₁－x₂－＝(x₁－x₂)．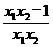

　当1＜x₁＜x₂时，x₁x₂＞1，x₁x₂－1＞0，从而f(x₁)－f(x₂)＜0，即f(x₁)＜f(x₂)．　

∴函数f(x)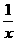＝+x在(1，+∞)上为增函数．

5．若f(x)是偶函数，其定义域为R且在[0，+∞)上是减函数，则f(－)与

f(a²－a+1)的大小关系是____．

4．已知f(x)＝x⁵+ax³+bx－8，f(－2)＝10，则f(2)=____．

3．设f(x)是R上的偶函数，且在(0，+∞)上是减函数，若x₁＜0且x₁+x₂＞0，则(　)

　　　　 A．f(－x₁)＞f(－x₂)　　　　　　　　　 B．f(－x₁)＝f(－x₂)

　　　　 C．f(－x₁)＜f(－x₂)　　　　　　　　　 D．f(－x₁)与f(－x₂)大小不确定

2．设定义在R上的函数f(x)＝｜x｜，则f(x)(　)

　　　　 A．既是奇函数，又是增函数　　　　　　 B．既是偶函数，又是增函数

　　　　 C．既是奇函数，又是减函数　　　　　　 D．既是偶函数，又是减函数

7．设f(x)是定义在R上的增函数，f(xy)＝f(x)+f(y)，f(3)＝1，

求解不等式f(x)+f(x－2)＞1．

七1．y＝f(x)(x∈R)是奇函数，则它的图象必经过点(　)

　A．(－a，－f(－a))　 B．(a，－f(a))　　　 C．(a，f(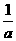))　 D．(－a，－f(a))

6．快艇和轮船分别从A地和C地同时开出，如右图，各沿箭头方向航行，快艇和轮船的速度分别是45千米/时和15千米/时，已知AC＝150千米，经过多少时间后，快艇和轮船之间的距离最短？

5．确定函数y＝x+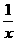(x＞0)的单调区间，并用定义证明．

4．函数f(x)＝2x²－3｜x｜的单调减区间是___________．