
题目列表(包括答案和解析)
5.若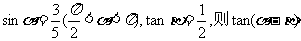 的值是
的值是
(A)2 (B)-2 (C) (D)
4.已知 =(5,-3),C(-1,3),
=(5,-3),C(-1,3),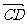 =2
=2 ,则点D的坐标为
,则点D的坐标为
(A)(11,9) (B)(4,0) (C)(9,3) (D)(9,-3)
3.设cosα=- ,α∈(0, π),则α的值可表示为
,α∈(0, π),则α的值可表示为
(A)arccos (B)-arccos
(B)-arccos (C)π-arccos
(C)π-arccos (D)π+arccos
(D)π+arccos
2.已知| |=8,
|=8, 为单位向量,当它们的夹角为
为单位向量,当它们的夹角为 时,
时, 在
在 方向上的投影为
方向上的投影为
(A)4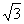 (B)4
(C)4
(B)4
(C)4 (D)8+
(D)8+
1.cos(- )的值是
)的值是
(A) (B)-
(B)- (C)
(C) (D)-
(D)-
C,李明的所有家人, D, 王明的好朋友
2,已知X={x|x>-4},则
A,0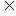 X B,{0}
X B,{0}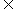 X C,
X C,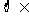 X
D,{0}
X
D,{0}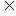 X
X
3:已知A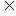 {1,2, ,4},且A中最多有一个偶数,这样的A集合有( )
{1,2, ,4},且A中最多有一个偶数,这样的A集合有( )
A,2 B,4, C,5 D,6
4:三个数70。3,0。37,,㏑0.3,的大小顺序是( )
A, 70。3,0。37,,㏑0.3, B, 70。3,,㏑0.3, 0。37
C, 0。37, , 70。3,,㏑0.3, D, ㏑0.3,, 70。3,0。37,
5:,如果二次函数y=5x2-nx-10在区间(- 是减函数,则n的值是( )
是减函数,则n的值是( )
A,1, B,-1, C,10, D,-10
6:下列函数中在区间(1,2)上是增函数的是( )
A,Y=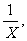 B,Y=X2+2X+1,
C,Y=-2X, D,Y=-2X2
B,Y=X2+2X+1,
C,Y=-2X, D,Y=-2X2
7:函数Y=-3X4是()
A,偶函数, B,奇函数, C,既是奇函数又是偶函数, D ,非奇非偶函数,
8:函数f(x)=(a2-3a+3)ax是指数函数 ,则a的值是( )
A,a=1或a=2
B,a=1 C,a=2
D,a>0或a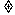 1
1
9:f(x)=㏑x+2x-5的零点一定位于以下的区间( )
A,(1,2) B,(2,3) C,(3,4) D,(4,5)
10:在区间(-2,2)上有零点且能用二分法求零点的是( )
A,Y=X2-2X-3 B,Y=X2-2X+1,
C,Y=X2-2X+3 D,Y=-X2+2X-3
11,某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程。在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( )
A,  B
B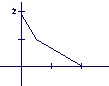
 C
C D
D 
12:指数函数Y=ax在区间(0,1)上的最大值的和是3,则a=( )
A,1/2 B,4 C,2 D,-10
二:填空题:
 13:计算㏒a1 +㏑e - 2
13:计算㏒a1 +㏑e - 2 =
=
 14:函数y=
14:函数y= 的定义域是
的定义域是
 15:若f(x)为偶函数,当 X>0时,f(x)=x,则当x<0时,f(x)=
15:若f(x)为偶函数,当 X>0时,f(x)=x,则当x<0时,f(x)=

 16:若指数函数f(x)与幂函数g(x)的图象相交于一点(2,4),则f(x)= ,g(x)=
16:若指数函数f(x)与幂函数g(x)的图象相交于一点(2,4),则f(x)= ,g(x)=
三:解答题:
17:设全集U为R,已知A={x|1<x<7},B={x|x<3或x>5},
求(1)A B (2)A
B (2)A B
(3)(CUA)
B
(3)(CUA) (CUB)
(CUB)
18:已知f(x)= ,证明f(x)在R上是奇函数。
,证明f(x)在R上是奇函数。
19:已知函数f(x)= ,(x
,(x 求这个函数的最大值和最小值
。
求这个函数的最大值和最小值
。
20:已知函数f(x)=㏒a , (a>0且a
, (a>0且a ,
,
求(1)函数的定义域。 (2)求使f(x)>0的x的取值范围。
21:经研究发现,学生的接受能力依赖于老师引入概念和描述总量所用的时间,开始讲题时,学生的兴趣保持较理想的状态,随后学生的注意力开始分散。分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力,x表示提出和讲授概念的时间(单位:分),有以下的公式:

(1),开讲后5分钟与开讲后20分钟比较,学生的接受能力何时强呢?
(2),开讲后多少分钟,学生的接受能力最强?能维持多长的时间?
(3),若讲解这道数学题需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲完这道题?
13. (0,0,3) 14.  15 y=2x或x+y-3=0 16. (x-2)2+(y+3)2=5
15 y=2x或x+y-3=0 16. (x-2)2+(y+3)2=5
三 解答题
17(12分) 已知△ABC三边所在直线方程为AB:3x+4y+12=0,BC:4x-3y+16=0,CA:2x+y-2=0
求AC边上的高所在的直线方程.
由 解得交点B(-4,0),
解得交点B(-4,0), . ∴AC边上的高线BD的方程
. ∴AC边上的高线BD的方程
为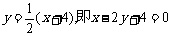 .
.
 18(12分) 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
18(12分) 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
 (1) FD∥平面ABC;
(1) FD∥平面ABC;
(2) AF⊥平面EDB.
(1)取AB的中点M,连FM,MC,
∵ F、M分别是BE、BA的中点 ∴ FM∥EA, FM=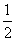 EA
EA
∵ EA、CD都垂直于平面ABC ∴ CD∥EA∴ CD∥FM
又 DC=a, ∴ FM=DC ∴四边形FMCD是平行四边形
∴ FD∥MC
FD∥平面ABC
(2) 因M是AB的中点,△ABC是正三角形,所以CM⊥AB
又 CM⊥AE,所以CM⊥面EAB, CM⊥AF, FD⊥AF,
因F是BE的中点, EA=AB所以AF⊥EB.
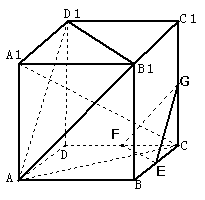 19(12分)如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,
19(12分)如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,
(1) 求证:平面A B1D1∥平面EFG;
(2) 求证:平面AA1C⊥面EFG.
20(12分) 已知圆C同时满足下列三个条件:①与y轴相切;②在直线y=x上截得弦长为2 ;③圆心在直线x-3y=0上.
求圆C的方程.
;③圆心在直线x-3y=0上.
求圆C的方程.
设所求的圆C与y轴相切,又与直线交于AB,
∵圆心C在直线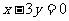 上,∴圆心C(3a,a),又圆
上,∴圆心C(3a,a),又圆
与y轴相切,∴R=3|a|. 又圆心C到直线y-x=0的距离
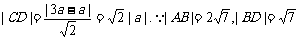
在Rt△CBD中, .
.
∴圆心的坐标C分别为(3,1)和(-3,-1),故所求圆的方程为
或 .
.
21(12分) 设有半径为3 的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
解:如图建立平面直角坐标系,由题意
可设A、B两人速度分别为3v千米/小时 ,
 v千米/小时,再设出发x0小时,在点P改变
v千米/小时,再设出发x0小时,在点P改变
方向,又经过y0小时,在点Q处与B相遇.
则P、Q两点坐标为(3vx0, 0),(0,vx0+vy0).
由|OP|2+|OQ|2=|PQ|2知,………………3分
(3vx0)2+(vx0+vy0)2=(3vy0)2,
即 .
.
 ……①………………6分
……①………………6分
将①代入 ……………8分
……………8分
又已知PQ与圆O相切,直线PQ在y轴上的截距就是两个相遇的位置.
设直线 相切,
相切,
则有 ……………………11分
……………………11分
答:A、B相遇点在离村中心正北 千米处………………12分
千米处………………12分
22(14分)已知圆C: 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1) 当l经过圆心C时,求直线l的方程;
(2) 当弦AB被点P平分时,写出直线l的方程;
(3) 当直线l的倾斜角为45º时,求弦AB的长.
(1)
已知圆C: 的圆心为C(1,0),因直线过点P、C,所以直线l的斜率为2,
的圆心为C(1,0),因直线过点P、C,所以直线l的斜率为2,
直线l的方程为y=2(x-1),即 2x-y-20.
(2)
当弦AB被点P平分时,l⊥PC,
直线l的方程为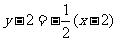 , 即 x+2y-6=0
, 即 x+2y-6=0
(3) 当直线l的倾斜角为45º时,斜率为1,直线l的方程为y-2=x-2 ,即 x-y=0
圆心C到直线l的距离为 ,圆的半径为3,
,圆的半径为3,
弦AB的长为 .
.
16.圆心在直线 上的圆C与
上的圆C与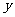 轴交于两点
轴交于两点 ,
,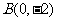 ,则圆C的方程为 .
,则圆C的方程为 .
15. 过点(1,2)且在两坐标轴上的截距相等的直线的方程 ___________;
14.已知正方形ABCD的边长为1,AP⊥平面ABCD,且AP=2,则PC= ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com