3、把10个水果分成3份，要求每份至少1个至多5个，则不同的分法数是　　　　　　　 (　　　　 )

A.5种　　　　 B.6种　　　　　 C.4种　　　　　　 D.3种

2、某幢四层大楼共有3个门，楼内有两个楼梯，那么由楼外到此楼的第四层的不同走法共有(　　　　 )

A.12种　　　 B.24种　　　　　 C.18种　　　　　 D.36种

1、某公共汽车上有10名乘客，要求在沿途的5个车站全部下完，乘客下车的可能方式有　 (　　　　 )

A.5¹⁰种　　　 B.10⁵种　　　　　 C.50种　　　　　 D.以上都不对

3、用两个原理解决实际问题时可按下列步骤进行思考：

(1)做什么事？--定目标；(2)怎么做？--定方法(分类、分步、先分类后分步、先分步后分类等)；

(3)确定每类或每步的方法数；(4)利用原理计算出方法总数并作答。

2、分步计数原理：完成一件事，需要分成n个步骤，做第一步有m₁种不同的方法，做第二步有m₂种不同的方法，……，做第n步有m_n种不同的方法，那么完成这件事共有的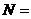　　　　　　　　　 种不同的方法。

分类计数原理与分步计数原理的区别在于　　　　　　　　　　　　　　　　　　　　　　　　　　 。

1、分类计数原理：完成一件事，有n类办法，在第一类办法中有m₁种不同的方法，第二类方法中有m₂种不同的方法，……，在第n类办法中有m_n 种不同的方法，那么完成这件事共有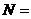：　　　　　　　 种不同的方法。

进一步理解分类计数原理与分步计数原理,并能灵活运用此原理解决实际问题。

10、电视台有8个节目准备分两天播出，每天播4个，(1)共有多少种不同播出方案？(2)若某电视剧必须于第一天播出，而一场体育比赛必须安排在第二天播出，则共有多少种不同的播出方案？

9、现将10张不同的电影票，8张不同的戏票和6张不同的球票分给3人，若每人只能取不同的票各一张，共有多少种不同的分配方案？

8、给出1、2、3、4四个数字，试问：(1)可组成多少个数字不重复的四位数？(2)可组成多少个数字不重复的自然数？(3)可组成多少个不超过四位的自然数？