
题目列表(包括答案和解析)
3、若实数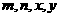 满足
满足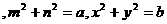 ,则
,则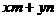 的最大值是 ( )
的最大值是 ( )
A.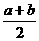 B.
B.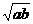 C.
C. 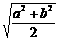 D.
D.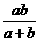
2、若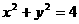 ,则
,则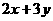 的最大值是
( )
的最大值是
( )
A.6 B.4 C.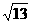 D.
2
D.
2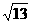
1、若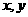 满足
满足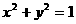 ,则
,则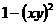 有
( )
有
( )
A. 最小值 和最大值1
B. 最小值
和最大值1
B. 最小值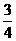 和最大值1
和最大值1
C. 最小值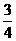 ,无最大值 D.
最大值1,无最小值
,无最大值 D.
最大值1,无最小值
4.判别式法:把待证不等式转化为一个一元二次函数的最大(小)值或值域问题,借助一元二次方程判别式来证明不等式,但要注意对二次项系数的讨论。
3、放缩法:把待证不等式的一边适当放大或缩小,利用不等式的传递性来证明不等式。放缩法常用的技巧:舍去一些项,在积中换大(或换小)某些项,扩大(或缩小)分式的分子(或分母)等。
2. 反证法:要证明不等式 ,先假设
,先假设 ,由题设及其他性质,推出矛盾,从而肯定
,由题设及其他性质,推出矛盾,从而肯定 成立。
成立。
用反证法证明不等式的一般步骤:①否定结论;②推理论证;③得出矛盾;④肯定结论。
1. 三角换元: (1)若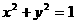 ,则可令x = cosq , y = sinq (
,则可令x = cosq , y = sinq (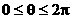 )。若
)。若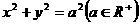 ,则可令x =
,则可令x =  cosq , y =
cosq , y =  sinq (
sinq (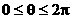 )。
)。
(2)若0≤x≤1,则可令x = sinq (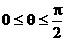 )或x = sin2q (
)或x = sin2q (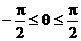 )。
)。
11、解关于x的不等式: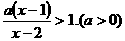
10、解下列不等式:
(1) (2)
(2)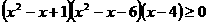
(3)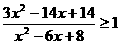 (4)
(4)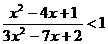
(5) (6)
(6)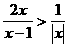
9、(1)不等式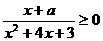 的解集是
的解集是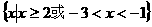 ,则
,则 ,
,
(2)不等式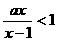 的解集是
的解集是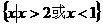 ,则实数a的取值范围是
,
,则实数a的取值范围是
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com