
题目列表(包括答案和解析)
8.5543除以8的余数是 ( )
A.-1 B.2 C.7 D.8
7.书架上有不同的数学书与不同的外文书共7本,现取2本数学书,1本外文书借给3位同学,每人一本,共有72种不同的借法,则数学书与外文书的本数分别为( )
A.4,3 B.3,4 C.5,2 D.2,5
6.从6名学生中,选出4人分别从事A、B、C、D四项不同的工作,若其中,甲、乙两人不能从事工作A,则不同的选派方案共有 ( )
A.96种 B.180种 C.240种 D.280种
5.设有编号为1,2,3,4,5的五个茶杯和编号为1,2,3,4,5的五个杯盖,将五个杯盖盖在五个茶杯上,至少有两个杯盖和茶杯的编号相同的盖法有( )
A.30种 B.31种 C.32种 D.36种
4.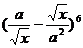 展开式中的第三项为
( )
展开式中的第三项为
( )
A.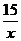 B.
B. C.
C.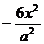 D.
D.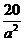
3.(1-x)2n-1展开式中,二项式系数最大的项是 ( )
A.第n-1项 B.第n项 C.第n-1项与第n+1项 D.第n项与第n+1项
2.若集合 是从M到N的映射,则满足
是从M到N的映射,则满足 的映射有 ( )
的映射有 ( )
A.6个 B.7个 C.8个 D.9个
1.n∈N*,则(20-n)(21-n)……(100-n)等于 ( )
A.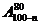 B.
B.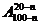 C.
C.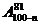 D.
D.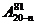
4.构造模型
例 4 共10级台阶,一人准备用8步走完,每步可走一级、二级或三级,共有多少种不同的走法?
练习:甲、乙两队各出7名队员,按事先排好的顺序出场参加围棋擂台赛,双方先由1号队员比赛,负者淘汰,胜者再与负方2号队员比赛,…,直到有一方队员全被淘汰为止,另一方获胜,形成一种比赛过程,那么所有可能出现的比赛过程有多少种?
☆5.转换说法
转换语言和变换说法,可以把比较隐晦的问题转化为直观问题,把抽象问题转化为具体的问题.
例5 已知集合A和集合B各含有12个元素,A∩B含有4个元素,试求同时满足下列两个条件的集合C的个数.
(1)C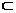 A∪B,且C中含有3个元素;
A∪B,且C中含有3个元素;
(2)C∩A≠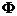 (
(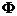 表示空集).
表示空集).
等价说法1
集合A有12个元素,集合B有8个元素,且A∩B=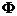 ,求在集合A∪B中取3个元素,其中至少含有A的1个元素构成的集合C的个数.
,求在集合A∪B中取3个元素,其中至少含有A的1个元素构成的集合C的个数.
为了更形象地理解题意,找出相应的实际问题作为模型,这样更有利于推进问题的解决。
显然,本题与下列实际问题等价.
等价说法2
某建筑队只会瓦工或只会木工的各有8人,同时既会瓦工又会木工的有4人,现从中挑选3人,至少有一人会瓦工,有多少种不同选法?
由于对于集合C中所含有的集合A的元素,无需考虑它是否属于A∩B,故本题还有另一等价说法.
等价说法3
有男生12人,女生8人,从中选取3人作代表出席一次会议,代表中至少有1名男生,问有多少种选法?
解法1 (分类法)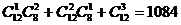 .
.
解法2 (排除法) 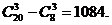
即集合C有1084个。
3.化归处理
通过构造模型可以将陌生问题,转化为常见题型的方法来处理。
例3 6人带10瓶汽水参加春游,每人至少带1瓶汽水,有多少种不同的带法?
练习:(1)求方程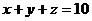 的正整数解的个数。
的正整数解的个数。
(2)有9名实习老师准备分到高二年级的6个班中实习,每班至少1名,共有多少种不同的分法?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com