
题目列表(包括答案和解析)
3、如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于 ( )
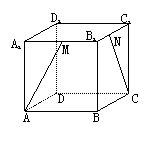
 (A)90° (B)45° (C)60°
(D)30°
(A)90° (B)45° (C)60°
(D)30°
2、异面直线a、b成60°,直线c⊥a,则直线b与c所成的角的范围为 ( )
(A)[30°,90°] (B)[60°,90°] (C)[30°,60°] (D)[60°,120°]
1、设a, b, c是空间的三条直线,下面给出三个命题:① 如果a, b是异面直线,b, c是异面直线,则a, c是异面直线;② 如果a, b相交,b, c也相交,则a, c相交;③ 如果a, b共面,b, c也共面,则a, c共面.
上述命题中,真命题的个数是 ( )
(A)3个 (B)2个 (C)1个 (D)0个
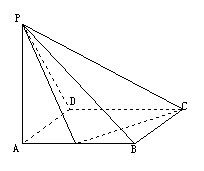
14. 已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,
∠ADB=60°,E、F分别是AC、AD上的动点,且
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
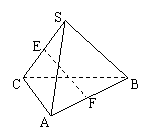
13. 如图,P是边长为a的正方形ABCD外一点,PA⊥平面ABCD,E为AB的中点,且PA=AB.
如图,P是边长为a的正方形ABCD外一点,PA⊥平面ABCD,E为AB的中点,且PA=AB.
(1)求证:平面PCE ⊥平面PCD;(2)求点D到平面PCE的距离.
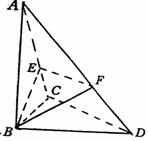
12.在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2.”拓展到空间,类比平面几何的勾股定理,研究三棱锥的面面积与底面面积间的关系。可以得出的正确结论是:“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两相互垂直,则 ”.
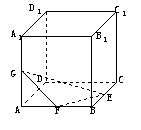
11.如图,在棱长为1的正方体ABCD-A1B1C1D1中,G、E分别为BB1、C1D1的中点,点F是正方形ADD1A1的中心,则四边形BGEF在正方体六个面内的射影图形的面积的最大值为 .
10. 在直二面角α-l-β中,A∈α,B∈β,AB与α所成的角为
在直二面角α-l-β中,A∈α,B∈β,AB与α所成的角为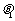 ,AB与β所成的角为
,AB与β所成的角为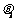 ,AB与l所成的角为
,AB与l所成的角为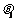 ,则
,则 =
.
=
.
9.如图所示,E、F、G是正方体ABCD-A1B1C1D1相应棱的中点,则(1)面EFG与面ABCD所成的角为 ;(2)面EFG与面ADD1A1所成的角为 .
8.在矩形ABCD中,AB=a,AD=2b,a<b,E、F分别是AD、BC的中点,以EF为折痕把四边形EFCD折起,当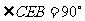 时,二面角C-EF-B的平面角的余弦值等于
(
)
时,二面角C-EF-B的平面角的余弦值等于
(
)
 A.0 B.
A.0 B.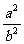 C.
C.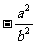 D.
D.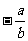
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com