20．(14分)设M是圆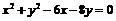上动点，O是原点，N是射线OM上点，

若|OM|·|ON|＝120，求N点的轨迹方程．

19．(14分)四棱锥P－ABCD中，底面ABCD是正方形，边长为a，PD=a，PA=PC=，

　 (1)求证：PD⊥平面ABCD；

　 (2)求证，直线PB与AC垂直；

　 (3)求二面角A－PB－D的大小；

　 (4)在这个四棱锥中放入一个球，求球的最大半径；

　 (5)求四棱锥外接球的半径．

18．(12分)自点P(－3，3)发出的光线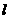经过x轴反射，其反射光线所在直线正好与圆

相切，求入射光线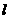所在直线的方程．

17．(12分)已知方程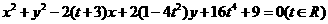的图形是圆.

　 (1)求t的取值范围；

　 (2)求其中面积最大的圆的方程．

16．(12分)某房地产公司要在荒地ABCDE上划出一块长方形地面(不改变方位)建造一幢

八层楼的公寓，问如何设计才能使公寓占地面积最大？并求出最大面积(精确到1m²).

　　　　　　　　　　　　　　　　　　　　　　 E　　　　　　 100m　　　　　　 D

　60m　　　　　　　　　　　　　　 80m

　　　　　　　　　　　　　　　　　　　　　　 A

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B　　　　 70m　　 C

15．(12分)已知两条直线l₁ = x + my + 6 = 0, l₂: (m－2)x + 3y + 2m = 0，问：当m为何值时, l₁与l₂(i)相交; (ii)平行; (iii)重合．

14．已知m、l是直线, 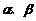是平面, 给出下列命题:

　　　 ①若l垂直于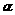内的两条相交直线, 则;

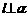　　　 ②若l平行于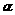, 则l平行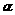内所有直线;

　　　 ③若;

　　　 ④若;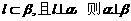

　　　 ⑤若∥l．

　　　 其中正确的命题的序号是　　　　　　　　　　　　 (注: 把你认为正确的命题的序号都填上)．

13．光线由点(－1，4)射出，遇直线2x+3y－6=0被反射，已知反射光线过点(3 ，)，反射光线所在直线方程__________________．

12．过点P(3，6)且被圆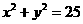截得的弦长为8的直线方程为　　　　 　　　　　．

11．将边长为的正方形钢板适当剪裁，再焊接成一个密闭的正四棱柱水箱，并要求这个水箱的全面积等于该正方形钢板的面积(要求剪裁的块数尽可能少，不计焊接缝的面积)，则该水箱的容积为　　　　　　　　　 ．