22. (本题满分12分)某种商品在30天内的销售价格P(元)与时间t天的函数关系用图甲表示，该商品在30天内日销售量Q(件)与时间t天之间的关系如下表所示：

(1)根据所提供的图像(图甲)写出该商品每件的销售价格P与时间t的函数关系式；

(2)在所给的直角坐标系(图乙)中，根据表中所提供的数据描出实数对(t，Q)的对应点，并确定一个日销售量Q与时间t的函数关系式。

(3)求该商品的日销售金额的最大值，并指出日销售金额最大的一天是30天中的第几天？(日销售金额＝每件的销售价格×日销售量)

t(天)	3	15	20	30
Q(件)	35	25	20	10

21.(本小题12分)

对于函数f(x)，若存在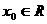，使f(x_o)＝x_o成立，则x_o为f(x)的不动点；

已知f(x)=ax²+(b+1)x+(b-1) (

(1)　　 当a＝1，b＝-2时，求f(x)的不动点；

(2)　　 若对于，函数f(x)恒有两个互异的不动点，求实数a的取值范围。

20.(本小题12分)

设f(x)为定义在R上的偶函数，当时，y＝x；当x>2时，y＝f(x)的图像时顶点在P(3,4),

　 且过点A(2,2)的抛物线的一部分

(1)　　　 求函数f(x)在上的解析式；

(2)　　　 在下面的直角坐标系中直接画出函数f(x)的图像；

(3)　　　 写出函数f(x)值域。

19.(本小题11分)

已知函数f(x)＝

(1)　　　 求证：；

(2)　　　 若＝1，，求f(a)的值。

18.(本小题10分)

已知函数若f(x)满足f(-x)＝－f(x)

(1)　　 求实数a的值；

(2)　　 判断并证明函数f(x)的单调性。

17、本小题满分11分

已知全集U=，集合A={，集合B＝

求(1)　 (2) ()　　　 (3)

15.若集合A　 {2,3,7},且A中之多有1个奇数，则这样的集合共有__________.

16一水池优2个进水口，1个出水口，进水速度如图甲、乙

　所示，某天0点到6点，该水池的蓄水量如图丙所示

给出以下3个论断(1)0点到3点只进水不出水；(2)3点到4点不进水只出水；(3)3点到6点不进水不出水。则一定正确的论断序号是___________.

第II卷

14.已知，则___________.

13.如果指数函数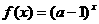是R上的减函数，则a的取值范围是　___________.

12.某公司在甲乙两地同时销售一种品牌车，利润(单位：万元)分别为L₁=-x²+21x和L₂＝2x其中

销售量(单位：辆)若该公司在两地共销售15辆，则能获得的最大利润为(　　)万元

A .90　　　B.60　　　　 C.120　　　 D.120.25