
题目列表(包括答案和解析)
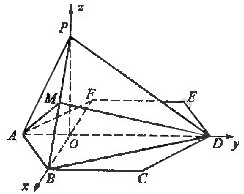
2. 如图,P是边长为1的正六边形ABCDEF所在平面外一点,
如图,P是边长为1的正六边形ABCDEF所在平面外一点, ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明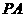 ⊥
⊥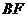 ;
;
(Ⅱ)求面 与面
与面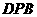 所成二面角的大小。
所成二面角的大小。
[解]本小题主要考察直线与平面的位置关系、二面角及其平面角等有关知识,考察思维能力和空间想象能力;考查应用向量知识解决立体几何问题的能力。满分12分。
方法一:
连结AD,则易知AD与BF的交点为O。
(I)证法1:
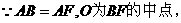

又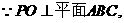
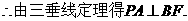
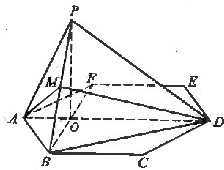 证法2:
证法2:
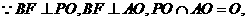
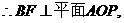
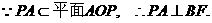
(II)设M为PB的中点,连结AM,MD。
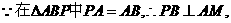
 斜线PB在平面ABC内的射影为OB,
斜线PB在平面ABC内的射影为OB,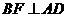 。
。

又

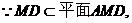

因此, 为所求二面角的平面角。
为所求二面角的平面角。
在正六边形ABCDEF中,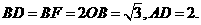
在Rt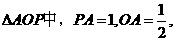
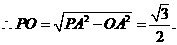
在Rt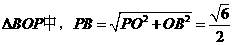 ,则
,则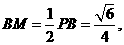
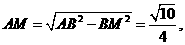
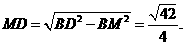
 在
在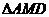 中,由余弦定理得
中,由余弦定理得
因此,所求二面角的大小为
方法二:
由题设条件,以O为原点建立空间直角坐标系O-xyz,如图。由正六边形的性质,可得
 在
在 中,
中, 故
故 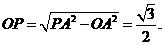
因而有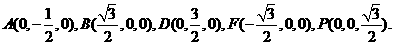
(I)证明:因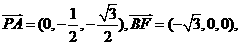 故
故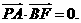 所以
所以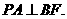
(II)设M为PB的中点,连结AM, MD, 则M点的坐标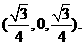
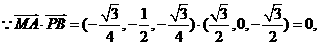
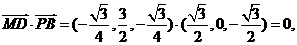

 因此,
因此, 为所求二面角的平面角。
为所求二面角的平面角。
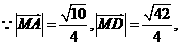
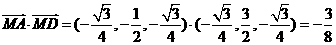
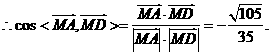
因此,所求二面角的大小为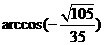 。
。
1. 如图所示,
如图所示,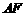 、
、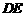 分别是
分别是 、
、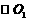 的直径,
的直径, 与两圆所在的平面均垂直,
与两圆所在的平面均垂直,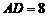 .
. 是
是 的直径,
的直径,
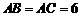 ,
,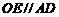 。
。
(I)求二面角 的大小;
的大小;
(II)求直线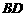 与
与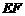 所成的角.
所成的角.
[解](I)∵AD与两圆所在的平面均垂直,
∴AD⊥AB,AD⊥AF,
故∠BAF是二面角B-AD-F的平面角,
依题意可知,ABFC是正方形,所以∠BAF=450.
即二面角B-AD-F的大小为450;
(II)以O为原点,BC、AF、OE所在直线为坐标轴,建立空间直角坐标系(如图所示),则
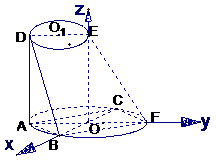
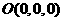 ,
,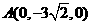 ),
), ,
,
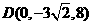 ,
,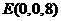 ,
,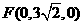
所以,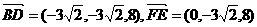
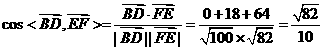 设异面直线BD与EF所成角为
设异面直线BD与EF所成角为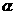 ,
,
则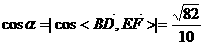 。
。
直线BD与EF所成的角为 。
。
10.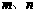 是空间两条不同直线,
是空间两条不同直线, 是空间两条不同平面,下面有四个命题:
是空间两条不同平面,下面有四个命题:
① ②
②
③ ④
④
其中真命题的编号是 (写出所有真命题的编号)。
9.已知正四棱椎的体积为12,地面的对角线为 ,则侧面与底面所成的二面角为____________。
,则侧面与底面所成的二面角为____________。
8.若一条直线与一个正四棱柱各个面所成的角都为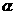 ,则
,则 =_____。
=_____。
7.(如图,在6题上)正四面体ABCD的棱长为l,棱AB∥平面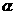 ,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是____________。
,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是____________。
6.如图(同理科图),在正三棱柱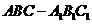 中,
中,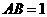 .若二面角
.若二面角
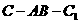 的大小为
的大小为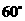 ,则点
,则点 到直线
到直线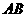 的距离为 。
的距离为 。
5.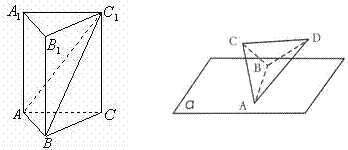 如图,在正三棱柱
如图,在正三棱柱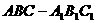 中,
中, .若二面角
.若二面角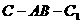 的大小为
的大小为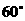 ,则点
,则点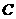 到平面
到平面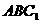 的距离为______________。
的距离为______________。
4.已知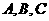 三点在球心为
三点在球心为 ,半径为
,半径为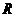 的球面上,
的球面上,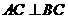 ,且
,且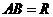 ,那么
,那么 两点的球面距离为 ,球心到平面
两点的球面距离为 ,球心到平面 的距离为______________。
的距离为______________。
3.如图,在正三棱柱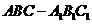 中,所有棱长均为1,则点
中,所有棱长均为1,则点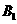 到平面
到平面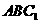
的距离为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com