
题目列表(包括答案和解析)
22. [06全国Ⅰ·理] 如图,
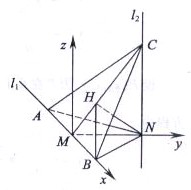
[06全国Ⅰ·理] 如图, 、
、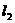 是互相垂直的异面直线,MN是它们的公垂线段。点A、B在
是互相垂直的异面直线,MN是它们的公垂线段。点A、B在 上,C在
上,C在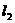 上,AM=MB=MN。
上,AM=MB=MN。
(Ⅰ)证明AC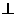 NB
NB
(Ⅱ)若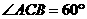 ,求NB与平面ABC所成角的余弦值.
,求NB与平面ABC所成角的余弦值.
[解] 解法一:
(Ⅰ)
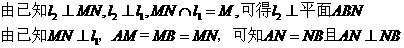 又AN为AC在平面ABN内的射影
又AN为AC在平面ABN内的射影
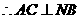
(Ⅱ)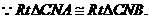
 又已知
又已知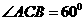 ,因此
,因此 为正三角形.
为正三角形.
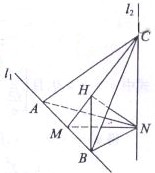
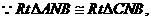
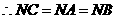 ,因此N在平面ABC内的射影H是正三角形ABC的中心,连结BH,
,因此N在平面ABC内的射影H是正三角形ABC的中心,连结BH, 为NB与平面ABC所成的角.
为NB与平面ABC所成的角.
 在
在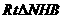 中,
中,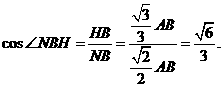
解法二:
如图,建立空间直角坐标系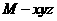 . 令
. 令 ,
,
则有A(-1,0,0),B(1,0,0),N(0,1,0)。
(Ⅰ) 是
是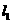 、
、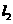 的公垂线,
的公垂线,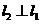 ,
,
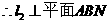

故可设C(0,1,m)。
于是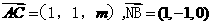
 ,
, 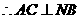 。
。
(Ⅱ)

又已知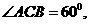
 为正三角形,
为正三角形,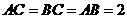 。
。
在 中,
中,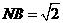 ,可得
,可得 ,故 C(0,1,
,故 C(0,1,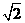 )
)
连结MC,做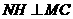 于H,设
于H,设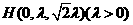
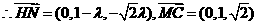
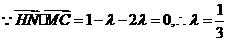
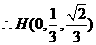 ,可得
,可得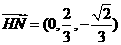 ,连结BH,则
,连结BH,则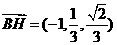 ,
,
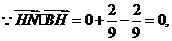
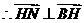 , 又
, 又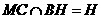

又
 。
。
21.[06辽宁·理] 已知正方形 。
。 、
、 分别是
分别是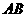 、
、 的中点,将
的中点,将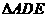 沿
沿 折起,如图所示。记二面角
折起,如图所示。记二面角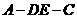 的大小为
的大小为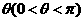 。
。
(I) 证明 平面
平面 ;
;
(II) 若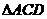 为正三角形,试判断点
为正三角形,试判断点 在平面
在平面 内的射影
内的射影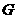 是否在直线
是否在直线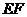 上,证明你的结论,并求角
上,证明你的结论,并求角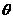 的余弦值。
的余弦值。
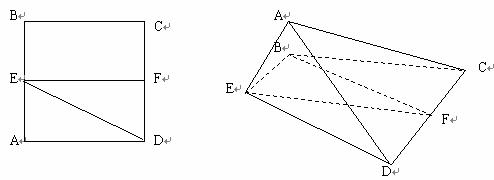
[解]
(I) 证明:EF分别为正方形ABCD得边AB、CD的中点,
 EB//FD,且EB=FD,
EB//FD,且EB=FD,
 四边形EBFD为平行四边形。
四边形EBFD为平行四边形。
 BF//ED
BF//ED
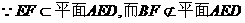

 平面
平面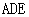 .
.
(II)解法1:
如右图,点A在平面BCDE内的射影G在直线EF上,
过点A作AG垂直于平面BCDE,垂足为G,连结GC,GD.

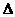 ACD为正三角形,
ACD为正三角形,  AC=AD
AC=AD  CG=GD
CG=GD
 G在CD的垂直平分线上,
G在CD的垂直平分线上,
 点A在平面BCDE内的射影G在直线EF上,
点A在平面BCDE内的射影G在直线EF上,
过G作GH垂直于ED于H,连结AH,则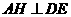 ,所以
,所以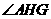 为二面角
为二面角
A-DE-C的平面角。即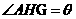 。
。
设原正方体的边长为2a,连结AF
在折后图的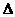 AEF中,AF=
AEF中,AF=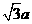 ,EF=2AE=2a,
,EF=2AE=2a,
即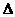 AEF为直角三角形,
AEF为直角三角形,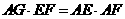 。
。
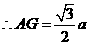
在Rt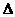 ADE中,
ADE中,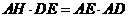
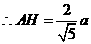
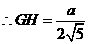
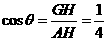 。
。
解法2:点A在平面BCDE内的射影G在直线EF上
连结AF,在平面AEF内过点作 ,垂足为
,垂足为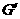 。
。

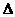 ACD为正三角形,F为CD的中点,
ACD为正三角形,F为CD的中点, 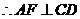
又因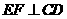 , 所以
, 所以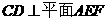
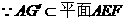
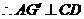
又 且
且
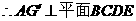
 为A在平面BCDE内的射影G.
为A在平面BCDE内的射影G.
即点A在平面BCDE内的射影在直线EF上
过G作GH垂直于ED于H,连结AH,则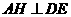 ,所以
,所以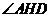 为二面角A-DE-C的平面角。即
为二面角A-DE-C的平面角。即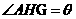
设原正方体的边长为2a,连结AF
在折后图的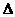 AEF中,AF=
AEF中,AF=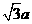 ,EF=2AE=2a,
,EF=2AE=2a,
即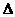 AEF为直角三角形,
AEF为直角三角形,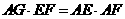
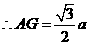
在Rt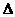 ADE中,
ADE中,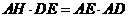
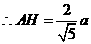
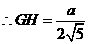
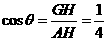 。
。
解法3:点A在平面BCDE内的射影G在直线EF上
连结AF,在平面AEF内过点作 ,垂足为
,垂足为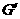 。
。

 ACD为正三角形,F为CD的中点,
ACD为正三角形,F为CD的中点,
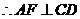
又因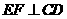 ,所以
,所以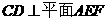
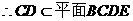

又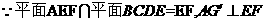

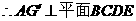
 为A在平面BCDE内的射影G。
为A在平面BCDE内的射影G。
即点A在平面BCDE内的射影在直线EF上。
过G作GH垂直于ED于H,连结AH,则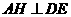 ,所以
,所以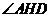 为二面角A-DE-C的平面角.即
为二面角A-DE-C的平面角.即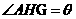 。
。
设原正方体的边长为2a,连结AF
在折后图的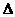 AEF中,AF=
AEF中,AF=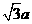 ,EF=2AE=2a,
,EF=2AE=2a,
即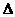 AEF为直角三角形,
AEF为直角三角形,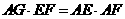
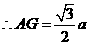
在Rt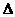 ADE中,
ADE中,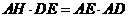
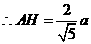
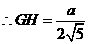 ,
,
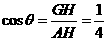 。
。
20.[06江西·文] 如图,已知三棱锥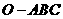 的侧棱
的侧棱 两两垂直,且OA=1,OB=OC=2,E是OC的中点。
两两垂直,且OA=1,OB=OC=2,E是OC的中点。
(1)求O点到面ABC的距离;
(2)求异面直线BE与AC所成的角;
(3)求二面角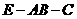 的大小。
的大小。
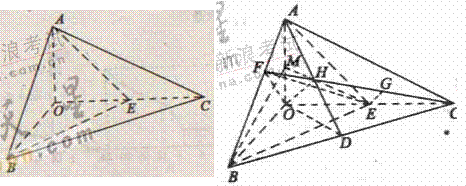
[解]方法一:(1)取BC的中点D,连AD、OD。
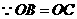 ,则
,则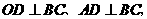
∴BC⊥面OAD。过O点作OH⊥AD于H,
则OH⊥面ABC,OH的长就是所要求的距离。
 ,
,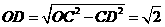 。
。
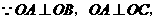 ∴
∴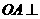 面OBC,则
面OBC,则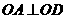 。
。
 ,在直角三角形OAD中,有
,在直角三角形OAD中,有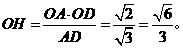
(另解:由 知:
知: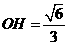 )
)
(2)取OA的中点M,连EM、BM,则EM∥AC,∠BEM是异面直线BE与AC所成的角。
求得: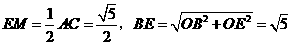 ,
,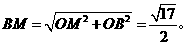
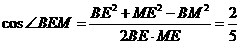 , ∴
, ∴ 。
。
(3)连结CH并延长交AB于F,连结OF、EF。
∵OC⊥面OAB, ∴OC⊥AB。 又∵OH⊥面ABC,
∴CF⊥AB ∴EF⊥AB,
则∠EFC就是所求二面角的平面角。作EG⊥CF于G,则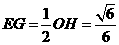 。
。
在直角三角形OEF中,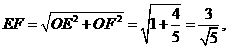
 (或表示为
(或表示为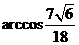 )
)
方法二:(1)以O为原点,OB、OC、OA分别为x、y、z轴建立空间直角坐标系。
则有A(0,0,1)、B(2,0,0)、C(0,2,0)、E(0,1,0)
设平面ABC的法向量为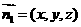 ,则由
,则由 知:
知: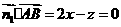 ,
,
则由 知:
知: ,
,
取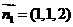 ,则点O到面ABC的距离为
,则点O到面ABC的距离为 。
。
(2)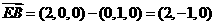 。
。 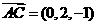
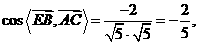 所以异面直线BE与AC所成的角
所以异面直线BE与AC所成的角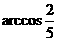 。
。
(3)设平面EAB的法向量为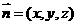 ,则由
,则由 知
知 ;
;
由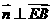 知:
知: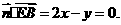 取
取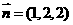 。
。
由(1)知平面ABC的法向量为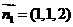 。
。
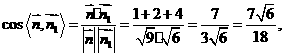
结合图形可知,二面角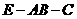 的大小为:
的大小为: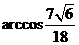 。
。
19.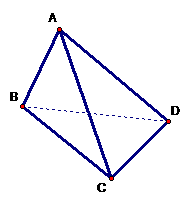 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD= ,BD=CD=1,另一个侧面是正三角形
,BD=CD=1,另一个侧面是正三角形
(1)求证:AD^BC;
(2)求二面角B-AC-D的大小;
(3)在直线AC上是否存在一点E,使ED与面BCD。
成30°角?若存在,确定E的位置;若不存在,说明理由。
[解] 解法一:
(1) 方法一:
作AH^面BCD于H,连DH。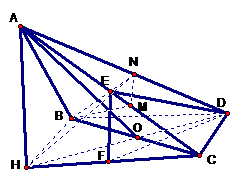
AB^BDÞHB^BD,又AD= ,BD=1
,BD=1
\AB=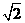 =BC=AC \BD^DC
=BC=AC \BD^DC
又BD=CD,则BHCD是正方形,
则DH^ BC
\AD^BC
方法二:取BC的中点O,连AO、DO
则有AO^BC,DO^BC, \BC^面AOD
\BC^AD
(2)作BM^AC于M,作MN^AC交AD于N,则ÐBMN就是二面角B-AC-D的平面角,因为AB=AC=BC=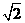 \M是AC的中点,且MN¤¤CD,则BM=
\M是AC的中点,且MN¤¤CD,则BM=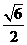 ,MN=
,MN=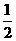 CD=
CD=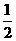 ,BN=
,BN=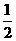 AD=
AD= ,由余弦定理可求得cosÐBMN=
,由余弦定理可求得cosÐBMN=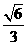
\ ÐBMN=arccos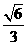 。
。
(3)设E是所求的点,作EF^CH于F,连FD。则EF¤¤AH,\EF^面BCD,ÐEDF就是ED与面BCD所成的角,则ÐEDF=30°。设EF=x,易得AH=HC=1,则CF=x,
FD=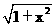 , \tanÐEDF=
, \tanÐEDF=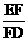 =
=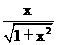 =
=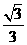 解得:x=
解得:x=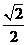 ,
,
则CE=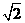 x=1
x=1
故线段AC上存在E点,且CE=1时,ED与面BCD成30°角。
解法二:此题也可用空间向量求解,解答略。
18. 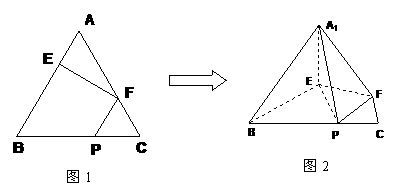 在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到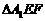 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示)。
[解][考点分析:本题主要考查线面垂直、直线和平面所成的角、二面角等基础知识,以及空间线面位置关系的证明、角和距离的计算等,考查空间想象能力、逻辑推理能力和运算能力]
不妨设正三角形的边长为3,则
(I)在图1中,取BE的中点D,连结DF,
∵AE∶EB=CF∶FA=1∶2,∴AF=AD=2,而∠A=60o,∴△ADF为正三角形。
又AE=DE=1,∴EF⊥AD。
在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的一个平面角,
由题设条件知此二面角为直二面角,∴A1E⊥BE。
又BE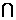 EF=E,∴A1E⊥面BEF,即A1E⊥面BEP。
EF=E,∴A1E⊥面BEF,即A1E⊥面BEP。
(II)在图2中,∵A1E不垂直于A1B,∴A1E是面A1BP的斜线,又A1E⊥面BEP,
∴A1E⊥BP,∴BP垂直于A1E在面A1BP内的射影(三垂线定理的逆定理)
设A1E在面A1BP内的射影为A1Q,且A1Q交BP于Q,
则∠EA1Q就是A1E与面A1BP所成的角,且BP⊥A1Q。
在△EBP中,∵BE=BP=2,∠EBP=60o,∴△EBP为正三角形,∴BE=EP。
又A1E⊥面BEP,∴A1B=A1P,∴Q为BP的中点,且EQ= ,而A1E=1,
,而A1E=1,
∴在Rt△A1EQ中,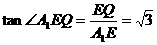 ,即直线A1E与面A1BP所成角为60o。
,即直线A1E与面A1BP所成角为60o。
(III)在图3中,过F作FM⊥A1P于M,连结QM、QF。
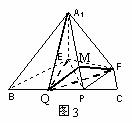 ∵CF=CP=1,∠C=60o,∴△FCP为正三角形,故PF=1,
∵CF=CP=1,∠C=60o,∴△FCP为正三角形,故PF=1,
又PQ=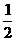 BP=1, ∴PF=PQ……
①
BP=1, ∴PF=PQ……
①
∵A1E⊥面BEP,EQ=EF= ,∴A1F=A1Q,
,∴A1F=A1Q,
∴△A1FP △A1QP,故∠A1PF=∠A1PQ…… ②
△A1QP,故∠A1PF=∠A1PQ…… ②
由①②及MP为公共边知△FMP △QMP,
△QMP,
故∠QMP=∠FMP=90°,且MF=MQ,
∴∠FMQ为二面角B-A1P-F的一个平面角。
在Rt△A1QP中,A1Q=A1F=2,PQ=1, ∴A1P=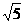 ,
,
∵MQ⊥A1P, ∴MQ=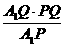
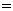
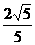 , ∴MF=
, ∴MF=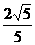 。
。
在△FCQ中,FC=1,QC=2,∠C=60o,由余弦定理得QF= ,
,
在△FMQ中,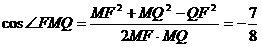 ,
,
∴二面角B-A1P-F的的大小为 。
。
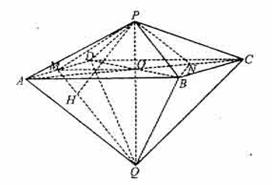
17. 如图4, 已知两个正四棱锥
如图4, 已知两个正四棱锥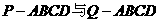 的高分别为1和2,
的高分别为1和2, 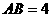 。
。
(I)证明:  ;
;
(II)求异面直线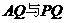 所成的角;
所成的角;
(III)求点 到平面
到平面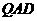 的距离。
的距离。
[解] 解法一:(Ⅰ)连接AC、BD,设AC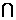 BD=O
BD=O
因为P-ABCD与Q-ABCD都是正四棱锥,
所以PO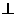 平面ABCD,QO
平面ABCD,QO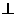 平面ABCD
平面ABCD
从而P、O、Q三点在一条直线上,所以PQ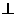 平面ABCD
平面ABCD
(II)由题设知,ABCD是正方形,所以 .由(I),
.由(I),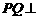 平面
平面 ,故可分别以直线CA、DB、QP为
,故可分别以直线CA、DB、QP为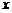 轴,
轴, 轴,
轴,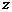 轴建立空间直角坐标系(如图),由题设条件,相关各点的坐标分别是
轴建立空间直角坐标系(如图),由题设条件,相关各点的坐标分别是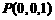 ,A(
,A(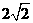 ,0,0),
,0,0),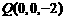 ,
,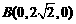



于是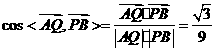
从而异面直线AQ与PB所成的角是 。
。
(Ⅲ)由(Ⅱ),点D的坐标是
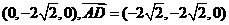 ,
,
 ,
,
设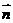 =(x,y,z)是平面QAD的一个法向量,由
=(x,y,z)是平面QAD的一个法向量,由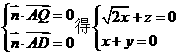
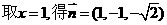
所以点P到平面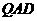 的距离
的距离 。
。
解法二:(Ⅰ)取AD的中点M,连接PM、QM。
因为P-ABCD与Q-ABCD都是正四棱锥,所以AD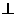 PM,AD
PM,AD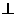 QM。
QM。
 从而AD
从而AD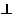 平面PQM。
平面PQM。
又PQ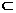 平面PQM,所以PQ⊥AD。
平面PQM,所以PQ⊥AD。
同理PQ⊥AB,所以PQ⊥平面ABCD。
(Ⅱ)连接AC、BD,设AC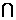 BD=O,由PQ
BD=O,由PQ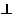 平面ABCD及正四棱锥的性质可知O在PQ上,从而P,A,Q,C四点共面。
平面ABCD及正四棱锥的性质可知O在PQ上,从而P,A,Q,C四点共面。
取OC的中点N,连接PN。
因为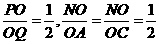 ,所以
,所以
 ,
, 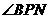 (或其补角)是异面直线AQ与PB所成的角。
(或其补角)是异面直线AQ与PB所成的角。
连接BN。 因为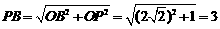 .
.
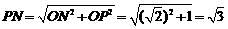
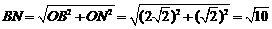
所以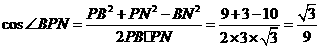 。
。
从而异面直线AQ与PB所成的角是 。
。
(Ⅲ)由(Ⅰ)知,AD⊥平面PQM,所以平面QAD⊥平面PQM 。
过点P作PH⊥QM于H,则PH⊥QAD,所以PH的长为点P到平面QAD的距离。
连结OM。因为OM=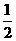 AB=2=OQ,所以∠MQP=45°。
AB=2=OQ,所以∠MQP=45°。
又PQ=PO+QO=3,于是PH=PQsin45°=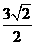 。
。
即点P到平面QAD的距离是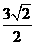 。
。
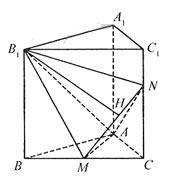
16. 如图,已知正三棱柱
如图,已知正三棱柱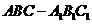 的侧棱长和底面边长为1,
的侧棱长和底面边长为1,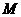 是底面
是底面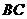 边上的中点,
边上的中点,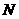 是侧棱
是侧棱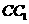 上的点,且
上的点,且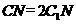 。
。
(Ⅰ)求二面角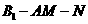 的平面角的余弦值;
的平面角的余弦值;
(Ⅱ)求点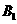 到平面
到平面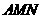 的距离。
的距离。
[解] 本小题主要考查线面关系、二面角和点到平面距离的有关知识及空间想象能力和推理运算能力。考查应用向量知识解决数学问题的能力。
 解法1:(Ⅰ)因为M是底面BC边上的中点,所以AM
解法1:(Ⅰ)因为M是底面BC边上的中点,所以AM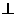 BC,又AM
BC,又AM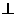
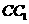 ,所以AM
,所以AM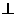 面
面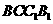 ,从而AM
,从而AM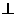
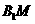 , AM
, AM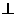 NM,所以
NM,所以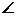
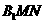 为二面角
为二面角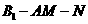 的平面角。又
的平面角。又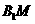 =
=
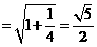 ,MN=
,MN=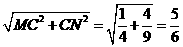 ,
,
连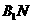 ,得
,得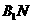 =
=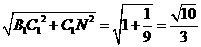 ,
,
在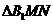 中,由余弦定理得
中,由余弦定理得
 。
。
故所求二面角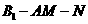 的平面角的余弦值为
的平面角的余弦值为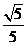 。
。
(Ⅱ)过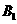 在面
在面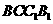 内作直线
内作直线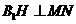 ,
,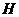 为垂足。又
为垂足。又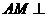 平面
平面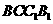 ,所以AM
,所以AM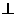
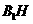 。于是
。于是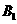 H
H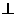 平面AMN,故
平面AMN,故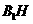 即为
即为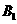 到平面AMN的距离。在
到平面AMN的距离。在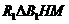 中,
中,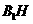 =
=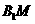
 。故点
。故点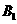 到平面AMN的距离为1。
到平面AMN的距离为1。
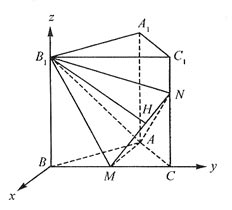 解法2:(Ⅰ)建立如图所示的空间直角坐标系,则
解法2:(Ⅰ)建立如图所示的空间直角坐标系,则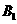 (0,0,1),M(0,
(0,0,1),M(0,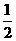 ,0),
,0),
C(0,1,0),N (0,1, ) ,A (
) ,A (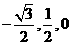 ),所以,
),所以,
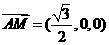 ,
,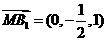 ,
, 。
。
因为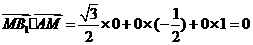
所以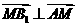 ,同法可得
,同法可得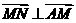 。
。
故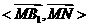 为二面角
为二面角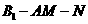 的平面角。
的平面角。
∴ 
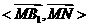 =
=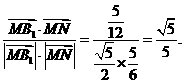
故所求二面角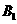 -AM-N的平面角的余弦值为
-AM-N的平面角的余弦值为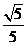 。
。
(Ⅱ)设 为平面AMN的一个法向量,则由
为平面AMN的一个法向量,则由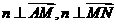 得
得
 故可取
故可取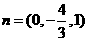 。
。
设 与n的夹角为
与n的夹角为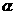 ,则
,则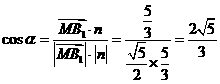 。
。
所以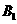 到平面AMN的距离为
到平面AMN的距离为 。
。
15.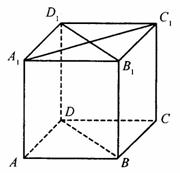 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m,
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m,
(I)试确定m,使得直线AP与平面BD D1B1所成角的正切值为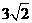 ;
;
(Ⅱ)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,并证明你的结论。
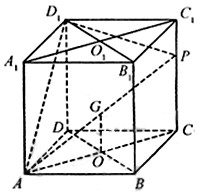 [解] 本小题主要考查线面关系、直线与平面所成角的有关知识及空间想像能力和推理运算能力。考查应用向量知识解决数学问题的能力。
[解] 本小题主要考查线面关系、直线与平面所成角的有关知识及空间想像能力和推理运算能力。考查应用向量知识解决数学问题的能力。
解法1:(I)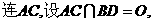
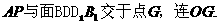
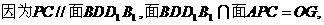
故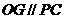 。所以
。所以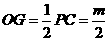 。
。
又 .
.
故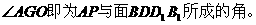
在 △
△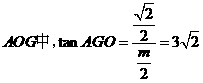 ,即
,即 .
.
故当 时,直线
时,直线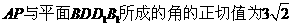 。
。
(Ⅱ)依题意,要在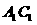 上找一点
上找一点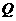 ,使得
,使得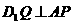 .
.
可推测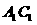 的中点
的中点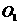 即为所求的
即为所求的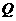 点。
点。
因为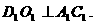
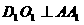 ,所以
,所以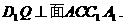
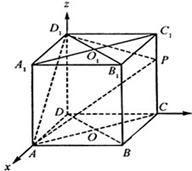 又
又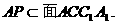 ,故
,故 。
。
从而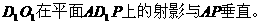
解法二:(I)建立如图所示的空间直角坐标系,则
A(1,0,0),B(1,1,0),P(0,1,m),C(0,1,0),
D(0,0,0),B1(1,1,1),D1(0,0,1).
所以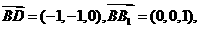
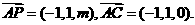
又由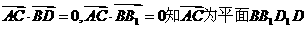 的一个法向量.
的一个法向量.
设 与
与 所成的角为
所成的角为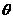 ,
,
则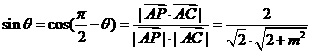
依题意有: ,解得
,解得 .
.
故当 时,直线
时,直线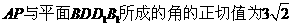 。
。
(Ⅱ)若在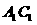 上存在这样的点
上存在这样的点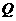 ,设此点的横坐标为
,设此点的横坐标为 ,
,
则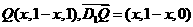 。
。
依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP。等价于

即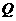 为
为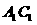 的中点时,满足题设的要求。
的中点时,满足题设的要求。
14.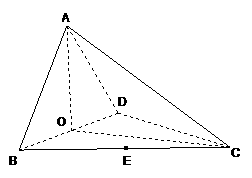 如图,四面体ABCD中,O、E分别是BD、BC的中点,
如图,四面体ABCD中,O、E分别是BD、BC的中点,
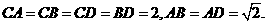
(I)求证: 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。
[解] 本小题主要考查直线与平面的位置关系、异面直线所成的角以及点到平面的距离基本知识,考查空间想象能力、逻辑思维能力和运算能力。
 方法一:(I)证明:连结OC
方法一:(I)证明:连结OC
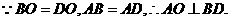
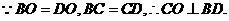
在 中,由已知可得
中,由已知可得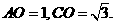
而

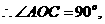 即
即

 平面
平面
(II)
取AC的中点M,连结OM、ME、OE,由E为BC的中点知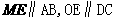
 直线OE与EM所成的锐角就是异面直线AB与CD所成的角
直线OE与EM所成的锐角就是异面直线AB与CD所成的角
在 中,
中,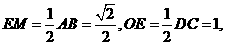
 是直角
是直角 斜边AC上的中线,
斜边AC上的中线,
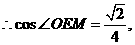
 异面直线AB与CD所成角的大小为
异面直线AB与CD所成角的大小为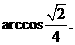
(III)
设点E到平面ACD的距离为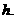
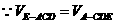 , ∴
, ∴ 
在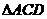 中,
中,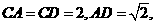
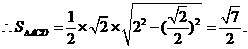
而
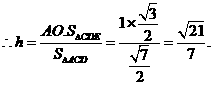
 点E到平面ACD的距离为
点E到平面ACD的距离为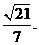
方法二:(I)同方法一。
(II)解:以O为原点,如图建立空间直角坐标系,则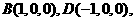
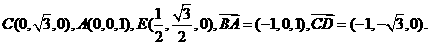
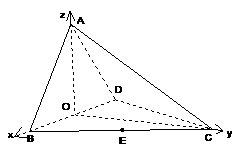
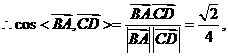
 异面直线AB与CD所成角的大小为
异面直线AB与CD所成角的大小为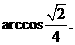
(III)解:设平面ACD的法向量为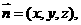 则
则

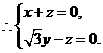
令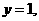 得
得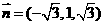 是平面ACD的一个法向量。
是平面ACD的一个法向量。
又
 点E到平面ACD的距离
点E到平面ACD的距离 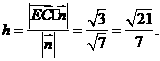
13.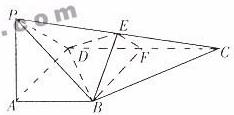 如图,在四棱锥
如图,在四棱锥 中,
中, 底面ABCD,
底面ABCD,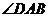 为直角,
为直角,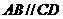 ,
,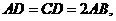 E、F分别为
E、F分别为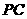 、
、 中点。
中点。
(I)试证: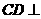 平面
平面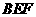 ;
;
(II)高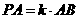 ,且二面角
,且二面角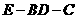 的平面角大小
的平面角大小 ,求
,求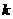 的取值范围。
的取值范围。
 [解] (I)证:由已知
[解] (I)证:由已知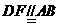 且
且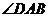 为直角。故ABFD是矩形。从而
为直角。故ABFD是矩形。从而 。又
。又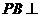 底面ABCD,
底面ABCD,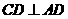 ,故由三垂线定理知
,故由三垂线定理知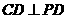 。在Rt
。在Rt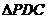 中,E、F分别为PC、CD的中点,故EF//PD,从而
中,E、F分别为PC、CD的中点,故EF//PD,从而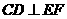 ,由此得
,由此得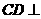 面BEF。
面BEF。
 (II)连接AC交BF于G,易知G为AC的中点,连接EG,则在
(II)连接AC交BF于G,易知G为AC的中点,连接EG,则在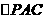 中易知EG//PA。又因PA
中易知EG//PA。又因PA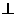 底面ABCD,故EG
底面ABCD,故EG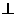 底面ABCD。在底面ABCD中,过G作GH
底面ABCD。在底面ABCD中,过G作GH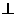 BD。垂足为H,连接EH,由三垂线定理知EH
BD。垂足为H,连接EH,由三垂线定理知EH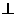 BD。从而
BD。从而 为二面角E-BD-C的平面角。
为二面角E-BD-C的平面角。
设 。
。
以下计算GH,考虑底面的平面图(如答(19)图2)。
连结GD,因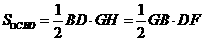 。
。
故GH=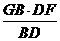 。在
。在 。
。
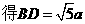 ,
而
,
而
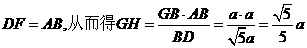 。因此,
。因此,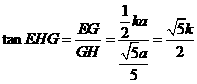 。
。
由 知
知 是锐角。故要使
是锐角。故要使
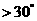 ,必须
,必须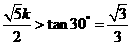 ,
,
解之得,上式中的取值范围为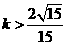 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com