
题目列表(包括答案和解析)
3.空间四边形ABCD中,若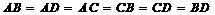 ,则
,则 与
与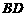 所成角为
所成角为
A、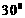 B、
B、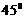 C、
C、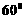 D、
D、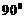
2.已知两个平面垂直,下列命题
①一个平面内的已知直线必垂直于另一个平面的任意一条直线;
②一个平面内的已知直线必垂直于另一个平面的无数条直线;
③一个平面内的任一条直线必垂直于另一个平面;
④过一个平面内任意一点作交线的垂线,则垂线必垂直于另一个平面.
其中正确的个数是( ) A.3 B.2 C.1 D.0
1.若直线a不平行于平面 ,则下列结论成立的是( )
,则下列结论成立的是( )
A.  内所有的直线都与a异面;
B.
内所有的直线都与a异面;
B.  内不存在与a平行的直线;
内不存在与a平行的直线;
C.  内所有的直线都与a相交;
D.直线a与平面
内所有的直线都与a相交;
D.直线a与平面 有公共点.
有公共点.
5.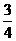 6.
6. 7.
7.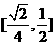 8.
8.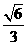 9.
9.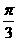 10.①,②
10.①,②
1.①③④⑤
2.①③ 3.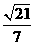 4.
4.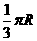
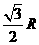
15.D 16.D 17.A 18.B
8.C 9.C 10.B 11.C 12.D 13.C 14.C
1.D 2.A 3.D 4.B 5.C 6.B 7.B
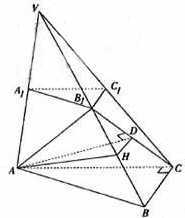
24.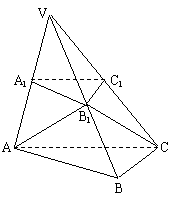 [06山东·理] 如图,已知平面
[06山东·理] 如图,已知平面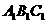 平行于三棱锥
平行于三棱锥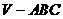 的底面ABC,等边△
的底面ABC,等边△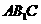 所在的平面与底面ABC垂直,且∠ACB=90°,设
所在的平面与底面ABC垂直,且∠ACB=90°,设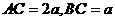
(Ⅰ)求证直线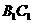 是异面直线
是异面直线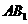 与
与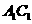 的公垂线;
的公垂线;
(Ⅱ)求点A到平面VBC的距离;
(Ⅲ)求二面角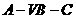 的大小。
的大小。
[解]解法1:(Ⅰ)证明: ∵平面
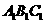 ∥平面
∥平面 ,
,

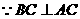
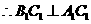
又∵平面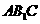 ⊥平面
⊥平面 ,平面
,平面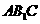 ∩平面
∩平面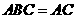 ,
,
∴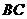 ⊥平面
⊥平面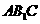 ,
,
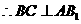
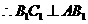 ,
,
 又
又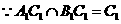 ,
,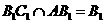 .
. 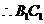 为
为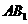 与
与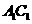 的公垂线.
的公垂线.
(Ⅱ)解法1:过A作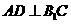 于D,
于D,
∵△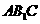 为正三角形, ∴D为
为正三角形, ∴D为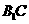 的中点.
的中点.
∵BC⊥平面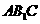 ∴
∴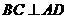 ,
,
又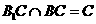 , ∴AD⊥平面
, ∴AD⊥平面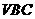 ,
,
∴线段AD的长即为点A到平面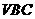 的距离.
的距离.
在正△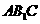 中,
中,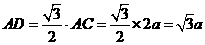 .
.
∴点A到平面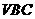 的距离为
的距离为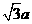 .
.
解法2:取AC中点O连结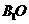 ,则
,则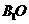 ⊥平面
⊥平面 ,且
,且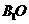 =
=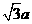 .
.
由(Ⅰ)知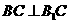 ,设A到平面
,设A到平面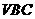 的距离为x,
的距离为x, 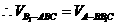 ,
,
即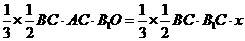 ,解得
,解得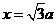 .
.
即A到平面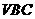 的距离为
的距离为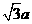 .
.
所以, 到平面
到平面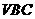 的距离为
的距离为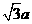 .
.
(III)
过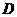 点作
点作 于
于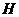 ,连
,连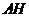 ,由三重线定理知
,由三重线定理知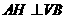
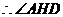 是二面角
是二面角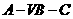 的平面角。
的平面角。
在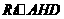 中,
中,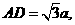
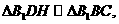
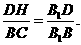
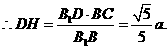
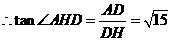 。
。
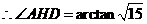 。
。
所以,二面角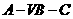 的大小为arctan
的大小为arctan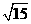 。
。
解法二:取 中点
中点 连
连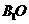 ,易知
,易知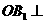 底面
底面 ,过
,过 作直线
作直线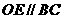 交
交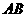 于
于 。
。
取 为空间直角坐标系的原点,
为空间直角坐标系的原点,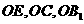 所在直线分别为
所在直线分别为 轴,
轴,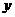 轴,
轴,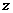 轴建立如图所示的空间直角坐标系。则
轴建立如图所示的空间直角坐标系。则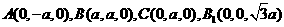 。
。
 (I)
(I)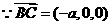 ,
,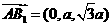 ,
,
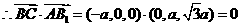 ,
,
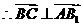 。
。 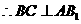
又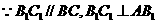
由已知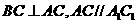 。
。
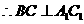 ,
,
而 。
。
又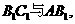
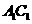 显然相交,
显然相交,
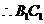 是
是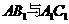 的公垂线。
的公垂线。
(II)设平面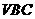 的一个法向量
的一个法向量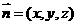 , 又
, 又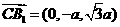
由
取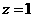 得
得 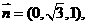
点 到平面
到平面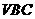 的距离,即
的距离,即 在平面
在平面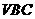 的法向量
的法向量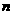 上的投影的绝对值。
上的投影的绝对值。
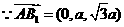 ,设所求距离为
,设所求距离为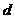 。
。
则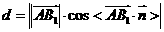

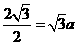
所以,A到平面VBC的距离为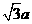 .
.
(III)设平面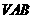 的一个法向量
的一个法向量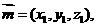
由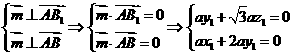 取
取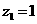 ,
,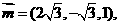
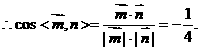
 二面角
二面角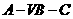 为锐角,
为锐角,
所以,二面角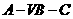 的大小为
的大小为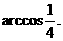
选择题与填空题答案
23.如图,在直三棱柱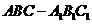 中,
中,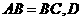 、
、 分别为
分别为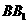 、
、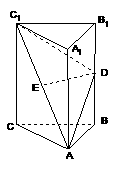
 的中点。
的中点。
(I)证明:ED为异面直线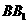 与
与 的公垂线;
的公垂线;
(II)设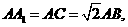 求二面角
求二面角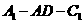 的大小。
的大小。
[解] 解法一:
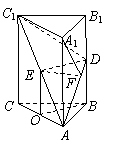 (Ⅰ)设O为AC中点,连接EO,BO,则EO∥=C1C,
(Ⅰ)设O为AC中点,连接EO,BO,则EO∥=C1C,
又C1C∥=B1B,所以EO∥=DB,EOBD为平行四边形,ED∥OB.
∵AB=BC,∴BO⊥AC,
又平面ABC⊥平面ACC1A1, BO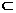 面ABC, 故BO⊥平面ACC1A1,
面ABC, 故BO⊥平面ACC1A1,
∴ED⊥平面ACC1A1, ED⊥AC1, ED⊥CC1,
∴ED⊥BB1,ED为异面直线AC1与BB1的公垂线.
(Ⅱ)连接A1E,由AA1=AC=AB 可知,A1ACC1为正方形,
∴A1E⊥AC1, 又由ED⊥平面ACC1A1和ED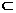 平面ADC1知
平面ADC1知
平面ADC1⊥平面A1ACC1,∴A1E⊥平面ADC1.作EF⊥AD,垂足为F,连接A1F,
则A1F⊥AD,∠A1FE为二面角A1-AD-C1的平面角.
不妨设AA1=2,则AC=2,AB=ED=OB=1,EF==,
tan∠A1FE=,∴∠A1FE=60°.
所以二面角A1-AD-C1为60°.
解法二:
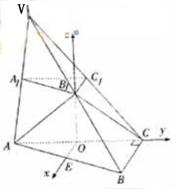
(Ⅰ)如图,建立直角坐标系O-xyz,其中原点O为AC的中点.
设A(a,0,0),B(0,b,0),B1(0,b,2c).
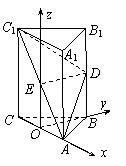 则C(-a,0,0),C1(-a,0,2c),E(0,0,c),D(0,b,c).
则C(-a,0,0),C1(-a,0,2c),E(0,0,c),D(0,b,c).
=(0,b,0),=(0,0,2c). ·=0,
∴ED⊥BB1.
又=(-2a,0,2c), ·=0, ∴ED⊥AC1,
所以ED是异面直线BB1与AC1的公垂线.
(Ⅱ)不妨设A(1,0,0),则B(0,1,0),C(-1,0,0),A1(1,0,2),
=(-1,-1,0),=(-1,1,0),=(0,0,2),
·=0,·=0,即BC⊥AB,BC⊥AA1,又AB∩AA1=A,
∴BC⊥平面A1AD.
又E(0,0,1),D(0,1,1),C(-1,0,1),=(-1,0,-1),=(-1,0,1),=(0,1,0),
·=0,·=0,即EC⊥AE,EC⊥ED,又AE∩ED=E, ∴ EC⊥面C1AD.
cos<,>==,即得和的夹角为60°.
所以二面角A1-AD-C1为60°.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com