
题目列表(包括答案和解析)
1.下列说法正确的是( )
A. 任何事件的概率总是在(0,1)之间
B. 频率是客观存在的,与试验次数无关
C. 随着试验次数的增加,频率一般会越来越接近概率
D. 概率是随机的,在试验前不能确定
1 从甲、乙、丙、丁四个人中选两名代表,求:
从甲、乙、丙、丁四个人中选两名代表,求:
(1)甲被选中的概率
(2)丁没被选中的概率
2 现有一批产品共有
现有一批产品共有 件,其中
件,其中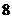 件为正品,
件为正品,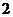 件为次品:
件为次品:
(1)如果从中取出一件,然后放回,再取一件,求连续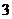 次取出的都是正品的概率;
次取出的都是正品的概率;
(2)如果从中一次取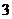 件,求
件,求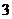 件都是正品的概率
件都是正品的概率
3 某路公共汽车
某路公共汽车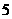 分钟一班准时到达某车站,求任一人在该车站等车时间
分钟一班准时到达某车站,求任一人在该车站等车时间
少于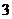 分钟的概率(假定车到来后每人都能上)
分钟的概率(假定车到来后每人都能上)
4 一个路口的红绿灯,红灯的时间为
一个路口的红绿灯,红灯的时间为 秒,黄灯的时间为
秒,黄灯的时间为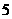 秒,绿灯的时间为
秒,绿灯的时间为
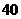 秒,当你到达路口时看见下列三种情况的概率各是多少?
秒,当你到达路口时看见下列三种情况的概率各是多少?
(1) 红灯 (2) 黄灯 (3) 不是红灯
数学3(必修) 第三章 概率 [基础训练A组]
1 有一种电子产品,它可以正常使用的概率为
有一种电子产品,它可以正常使用的概率为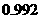 ,则它不能正常使用的概率是
,则它不能正常使用的概率是 
2 一个三位数字的密码键,每位上的数字都在
一个三位数字的密码键,每位上的数字都在 到
到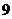 这十个数字中任选,某人忘记后一个号码,那么此人开锁时,在对好前两位数码后,随意拨动最后一个数字恰好能开锁的概率为___
这十个数字中任选,某人忘记后一个号码,那么此人开锁时,在对好前两位数码后,随意拨动最后一个数字恰好能开锁的概率为___
3 同时抛掷两枚质地均匀的硬币,则出现两个正面朝上的概率是
同时抛掷两枚质地均匀的硬币,则出现两个正面朝上的概率是

4 从五件正品,一件次品中随机取出两件,则取出的两件产品中恰好是一件正品,
从五件正品,一件次品中随机取出两件,则取出的两件产品中恰好是一件正品,
一件次品的概率是

5 在
在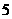 张卡片上分别写有数字
张卡片上分别写有数字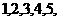 然后将它们混合,再任意排列成一行,则得到的数能被
然后将它们混合,再任意排列成一行,则得到的数能被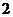 或
或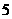 整除的概率是
整除的概率是

1 下列叙述错误的是( )
下列叙述错误的是( )
A.频率是随机的,在试验前不能确定,随着试验次数的增加,
频率一般会越来越接近概率
B. 若随机事件 发生的概率为
发生的概率为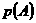 ,则
,则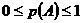
C. 互斥事件不一定是对立事件,但是对立事件一定是互斥事件
D
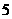 张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可能性相同
张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可能性相同
2 从三件正品、一件次品中随机取出两件,则取出的产品全是正品的概率是( )
从三件正品、一件次品中随机取出两件,则取出的产品全是正品的概率是( )
A
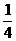 B
B
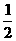 C
C
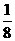 D
D 无法确定
无法确定
3 有五条线段长度分别为
有五条线段长度分别为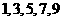 ,从这
,从这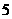 条线段中任取
条线段中任取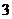 条,
条,
则所取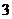 条线段能构成一个三角形的概率为( )
条线段能构成一个三角形的概率为( )
A
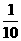 B
B
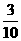 C
C
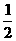 D
D
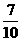
4 从
从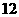 个同类产品(其中
个同类产品(其中 个是正品,
个是正品,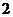 个是次品)中任意抽取
个是次品)中任意抽取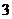 个的必然事件是( )
个的必然事件是( )
A.
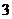 个都是正品 B
个都是正品 B 至少有
至少有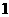 个是次品
个是次品
C
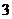 个都是次品 D
个都是次品 D 至少有
至少有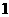 个是正品
个是正品
5 某产品分为甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为
某产品分为甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为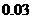 ,出现丙级品的概率为
,出现丙级品的概率为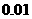 ,则对产品抽查一次抽得正品的概率是(
)
,则对产品抽查一次抽得正品的概率是(
)
A
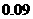 B
B
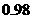
C
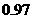 D
D
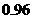
6 从一批羽毛球产品中任取一个,其质量小于
从一批羽毛球产品中任取一个,其质量小于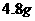 的概率为
的概率为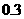 ,质量小于
,质量小于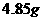 的概率为
的概率为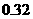 ,那么质量在
,那么质量在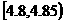 (
( 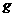 )范围内的概率是(
)
)范围内的概率是(
)
A
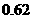 B
B
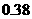 C
C
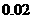 D
D
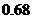
 则
则 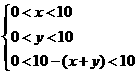 ,即
,即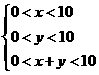 …4由一个三角形两边之和大于第三边,有
…4由一个三角形两边之和大于第三边,有
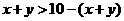 ,即
,即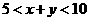 .
……6分
.
……6分
又由三角形两边之差小于第三边,有
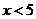 ,即
,即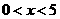 ,同理
,同理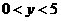 .
.
∴ 构造三角形的条件为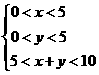 .
……8分
.
……8分
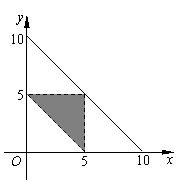
∴ 满足条件的点P(x,y)组成的图形是如图所示中的阴影区域(不包括区域的边界).
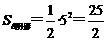 ,
,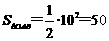 .∴
.∴ 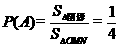 ……10分
……10分
18.基本事件的种数为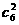 =15种 (Ⅰ)恰有一名参赛学生是男生的基本事件有
=15种 (Ⅰ)恰有一名参赛学生是男生的基本事件有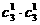 =9种
=9种  这一事件的概率P1=
这一事件的概率P1=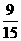 =0.6(5分)(Ⅱ)至少有一名参赛学生是男生这一事件是由两类事件构成的,即恰有一名参赛学生是男生和两名参赛学生都是男生
=0.6(5分)(Ⅱ)至少有一名参赛学生是男生这一事件是由两类事件构成的,即恰有一名参赛学生是男生和两名参赛学生都是男生 所求事件的概率P2=
所求事件的概率P2=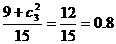 (9分)(Ⅲ)同理至多有一名参赛学生是男生的概率
(9分)(Ⅲ)同理至多有一名参赛学生是男生的概率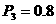
1 袋中有大小相同的红、黄两种颜色的球各
袋中有大小相同的红、黄两种颜色的球各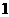 个,从中任取
个,从中任取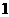 只,有放回地抽取
只,有放回地抽取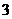 次
次 求:
求:
① 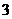 只全是红球的概率;
只全是红球的概率;
② 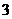 只颜色全相同的概率;
只颜色全相同的概率;
③ 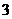 只颜色不全相同的概率
只颜色不全相同的概率
2 抛掷
抛掷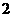 颗质地均匀的骰子,求点数和为
颗质地均匀的骰子,求点数和为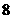 的概率
的概率
3 从
从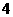 名男生和
名男生和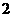 名女生中任选
名女生中任选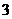 人参加演讲比赛,
人参加演讲比赛,
①求所选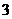 人都是男生的概率;
人都是男生的概率;
②求所选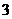 人恰有
人恰有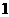 名女生的概率;
名女生的概率;
③求所选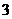 人中至少有
人中至少有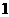 名女生的概率
名女生的概率
4 平面上画了一些彼此相距
平面上画了一些彼此相距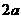 的平行线,把一枚半径
的平行线,把一枚半径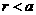 的硬币任意掷在这个平面上,求硬币不与任何一条平行线相碰的概率
的硬币任意掷在这个平面上,求硬币不与任何一条平行线相碰的概率
数学3(必修) 第三章 概率 [综合训练B组]
1 在
在 件产品中,
件产品中,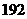 有件一级品,
有件一级品,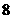 件二级品,则下列事件:
件二级品,则下列事件:
①在这 件产品中任意选出
件产品中任意选出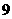 件,全部是一级品;
件,全部是一级品;
②在这 件产品中任意选出
件产品中任意选出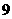 件,全部是二级品;
件,全部是二级品;
③在这 件产品中任意选出
件产品中任意选出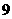 件,不全是一级品;
件,不全是一级品;
④在这 件产品中任意选出
件产品中任意选出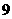 件,其中不是一级品的件数小于
件,其中不是一级品的件数小于 ,
,
其中 是必然事件; 是不可能事件; 是随机事件
2 投掷红、蓝两颗均匀的骰子,观察出现的点数,至多一颗骰子出现偶数点的概率是_____
投掷红、蓝两颗均匀的骰子,观察出现的点数,至多一颗骰子出现偶数点的概率是_____
3 在区间
在区间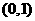 中随机地取出两个数,则两数之和小于
中随机地取出两个数,则两数之和小于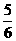 的概率是______________
的概率是______________
4 在
在 的水中有一个草履虫,现从中随机取出
的水中有一个草履虫,现从中随机取出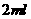 水样放到显微镜下观察,则发现草履虫的概率是_____________
水样放到显微镜下观察,则发现草履虫的概率是_____________
1 同时向上抛
同时向上抛 个铜板,落地时
个铜板,落地时 个铜板朝上的面都相同,你认为对这
个铜板朝上的面都相同,你认为对这 个铜板下面情况更可能正确的是( )
个铜板下面情况更可能正确的是( )
A 这
这 个铜板两面是一样的
个铜板两面是一样的
B 这
这 个铜板两面是不同的
个铜板两面是不同的
C 这
这 个铜板中有
个铜板中有 个两面是一样的,另外
个两面是一样的,另外 个两面是不相同的
个两面是不相同的
D 这
这 个铜板中有
个铜板中有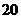 个两面是一样的,另外
个两面是一样的,另外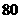 个两面是不相同的
个两面是不相同的
2 口袋内装有一些大小相同的红球、白球和黒球,从中摸出
口袋内装有一些大小相同的红球、白球和黒球,从中摸出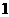 个球,摸出红球的概率是
个球,摸出红球的概率是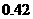 ,摸出白球的概率是
,摸出白球的概率是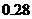 ,那么摸出黒球的概率是( )
,那么摸出黒球的概率是( )
A
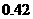 B
B
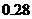 C
C
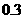 D
D
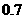
3 从装有
从装有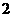 个红球和
个红球和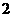 个黒球的口袋内任取
个黒球的口袋内任取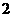 个球,那么互斥而不对立的两个事件是( )
个球,那么互斥而不对立的两个事件是( )
A 至少有一个黒球与都是黒球
B
至少有一个黒球与都是黒球
B 至少有一个黒球与都是黒球
至少有一个黒球与都是黒球
C 至少有一个黒球与至少有
至少有一个黒球与至少有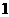 个红球 D
个红球 D 恰有
恰有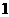 个黒球与恰有
个黒球与恰有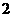 个黒球
个黒球
4 在
在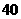 根纤维中,有
根纤维中,有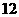 根的长度超过
根的长度超过 ,从中任取一根,取到长度超过
,从中任取一根,取到长度超过 的纤维的概率是( )
的纤维的概率是( )
A
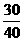 B
B
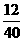 C
C
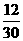 D
D 以上都不对
以上都不对
5 先后抛掷骰子三次,则至少一次正面朝上的概率是( )
先后抛掷骰子三次,则至少一次正面朝上的概率是( )
A
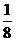 B
B
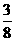 C
C
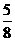 D
D
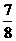
6 设
设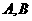 为两个事件,且
为两个事件,且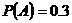 ,则当( )时一定有
,则当( )时一定有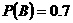
A
 与
与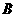 互斥 B
互斥 B
 与
与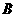 对立 C
对立 C
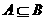 D
D
 不包含
不包含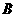
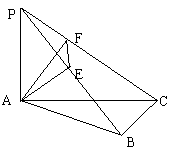
17.如图,PA⊥平面ABC,AE⊥PB,AB⊥BC,AF⊥PC,PA=AB=BC=2(1)求证:平面AEF⊥平面PBC;
(2)求二面角P-BC-A的大小;(3)求三棱锥P-AEF的体积.
15.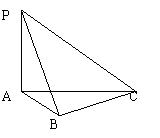 如图,PA⊥平面ABC,平面PAB⊥ 16.在三棱锥S-ABC中,已知AB=AC,平面PBC 求证:AB⊥BC
O是BC的中点,平面SAO⊥平面ABC
如图,PA⊥平面ABC,平面PAB⊥ 16.在三棱锥S-ABC中,已知AB=AC,平面PBC 求证:AB⊥BC
O是BC的中点,平面SAO⊥平面ABC
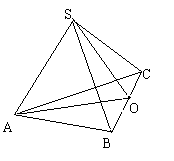 求证:∠SAB=∠SAC
求证:∠SAB=∠SAC
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com