
题目列表(包括答案和解析)
6.有以下结论:
(1)若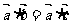 ,且
,且 ,则
,则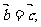
(2)
(3)
(4)函数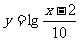 的图象可由函数
的图象可由函数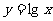 的图象按向量
的图象按向量 平移而得到。
平移而得到。
其中错误的结论是( )
A (1)(2) B (3)(4) C (1)(3) D (2)(4)
5.函数 的最小正周期是( )
的最小正周期是( )
A  B
B 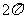 C
C 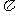 D
D 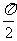
4.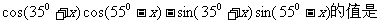 ( )
( )
A 0
B -1
C  D 1
D 1
3.设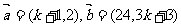 ,若
,若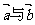 共线,则k等于( )
共线,则k等于( )
A 3 B 0 C -5 D 3或-5
2.已知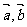 为单位向量,则下列正确的是( )
为单位向量,则下列正确的是( )
A 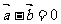 B
B 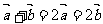 C
C  D
D 
1.sin(-11400)的值是( )
A  B
B  C
C  D
D 
22. (本小题10分)解关于x的不等式 >x,(a∈R).
>x,(a∈R).
解:由 >x得
>x得 -x>0即
-x>0即 >0(2分)
>0(2分)
此不等式与x(ax-1)>0同解.(3分)

 x>0 x<0
x>0 x<0
①若a<0,则 或
ax-1>0 ax-1<0
得: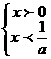 或
或
即 无解 或 <x<0. ∴解集为(
<x<0. ∴解集为( ,0).(4分)
,0).(4分)
②若a=0,则-x>0 x<0,∴解集为(-∞,0).(6分)
x<0,∴解集为(-∞,0).(6分)

 x>0 x<0
x>0 x<0
③若a>0,则 或
ax-1>0 ax-1<0
得 或
或
即:x> 或x<0,∴解集为(-∞,0)∪(
或x<0,∴解集为(-∞,0)∪( ,+∞)(9分)
,+∞)(9分)
综上所述:①当a<0时,不等式的解集是( ,0)
,0)
②当a=0时,不等式的解集是(-∞,0)
③当a>0时,不等式的解集是(-∞,0)∪( ,+∞)(10分)
,+∞)(10分)
21.(本题满分10分)
已知 ,
,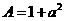 ,
,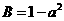 ,
, ,试比较
,试比较 、
、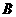 、
、 的大小.
的大小.
[解答]不妨设 ,则
,则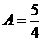 ,
,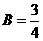 ,
,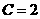 由此猜想
由此猜想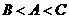
由 得
得 ,
,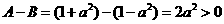 得
得 ,……5分
,……5分
 得
得 ,…..9分
,…..9分
即得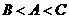 .………………………………………………………………………..10分
.………………………………………………………………………..10分
20. (本题满分14分)如图,△
(本题满分14分)如图,△ 的顶点
的顶点 在
在 正半轴上,顶点
正半轴上,顶点 在第一象限内,又知△
在第一象限内,又知△ 的面积为
的面积为 ,
, .
.
(Ⅰ)若向量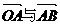 的夹角为
的夹角为 ,
,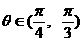 ,求
,求
实数 的取值范围;
的取值范围;
|
 在抛物线
在抛物线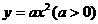 上,并且
上,并且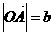 ,
, ,求使
,求使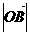 最小时实数
最小时实数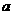 的值.
的值.
解:(Ⅰ)根据题意: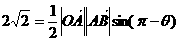
即  ,---------2分
,---------2分
又 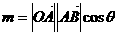
以上两式相除,并整理得:
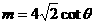 -----------4分
-----------4分
∵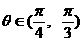 ,∴
,∴
∴实数 的取值范围是
的取值范围是 . -----------6分
. -----------6分
|
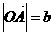 知点
知点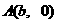 ,设点
,设点 ,则
,则
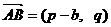 ,
,
于是
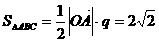 ,
, ,------8分
,------8分
又 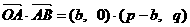

∴
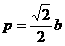 ,
-----------10分
,
-----------10分
从而 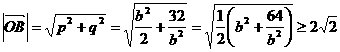 ,当且仅当
,当且仅当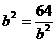 即
即 时,取等号, -----------12分
时,取等号, -----------12分
此时,点 ,代入
,代入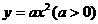 解得
解得 ,
,
∴ 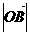 取得最小值
取得最小值 时,
时, . ------14分
. ------14分
(Ⅱ)解二:∵  ,
,
|
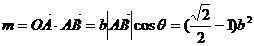 ,-------8分
,-------8分
∴  ,
,
∴ 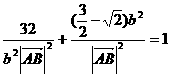 ,
,
即  ,-------10分
,-------10分
∴  ,
,
当且仅当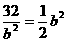 即
即 时,取等号,---------12分
时,取等号,---------12分
此时,点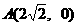 ,
,
由 求得点
求得点 纵坐标
纵坐标 ,
,
代入 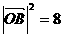 求得点
求得点 ,
,
代入 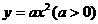 解得
解得 ,
,
∴ 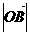 取得最小值
取得最小值 时,
时, .-------14分
.-------14分
19.(本大题满分12分) 已知函数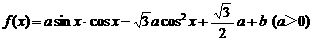 (1)写出函数的单调递减区间;
(2)设
(1)写出函数的单调递减区间;
(2)设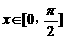 ,f (x)的最小值是-2,最大值是
,f (x)的最小值是-2,最大值是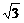 ,求实数a、b的
,求实数a、b的
(1)解:
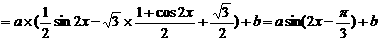 4分
∵a>0,x∈R,∴f (x)的递减区间是
4分
∵a>0,x∈R,∴f (x)的递减区间是 (k∈Z) 6分
(k∈Z) 6分
(2)解:∵x∈[0, ],∴2x∈[0,
],∴2x∈[0, ],2x-
],2x- ∈[
∈[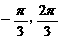 ] 7分
∴
] 7分
∴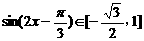 9分
∴函数f (x)的最小值是
9分
∴函数f (x)的最小值是 ,最大值是
,最大值是 10分
由已知得
10分
由已知得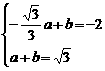 , 解得a=2,b=
, 解得a=2,b= 12分
12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com