
题目列表(包括答案和解析)
4、设全集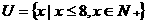 ,若
,若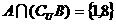 ,
,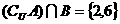 ,
,
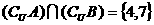 ,则
( )
,则
( )
(A)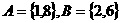 (B)
(B)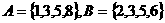
(C)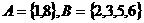 (D)
(D)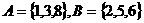
3、已知集合A={
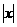 ≤2,
≤2,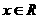 },B={
},B={ x≥a},且
x≥a},且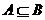 ,则实数a的取值范围是( )
,则实数a的取值范围是( )
(A)a≥-2 (B)a≤-2 (C)a≥2 (D)a≤2
2、下列各组中的两个集合M和N,表示同一集合的是 ( )
A. 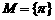 ,
, 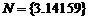 B.
B.
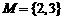 ,
, 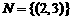
C. 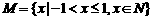 ,
, 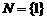 D.
D. 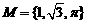 ,
, 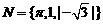
1、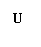 图中阴影部分表示的集合是
( )
图中阴影部分表示的集合是
( )
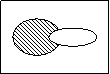

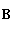
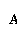 A.
A.  B.
B. 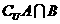
C. 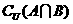 D.
D. 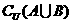
19、(本小题满分12分)
已知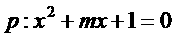 有两个不相等的负根,
有两个不相等的负根,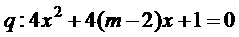 无实根,若“p或q”为真,“p且q”为假,求
无实根,若“p或q”为真,“p且q”为假,求 的取值范围。
的取值范围。
解:记p、q的解集分别为A、B。
∵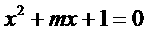 有两个不相等的负根,
有两个不相等的负根,
∴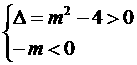 Þ
Þ
∴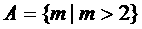
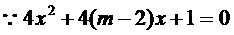 无实根,
无实根,
∴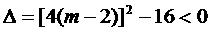
Þ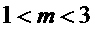
∴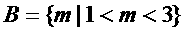
∵“p或q”为真,“p且q”为假
∴p,q中仅有一个为真。
∴(1)p真且q假,即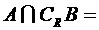
 ∩
∩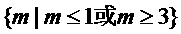
=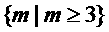
(2)p假且q真,即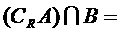
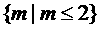 ∩
∩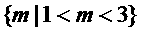
=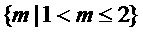
综上所述m的取值范围是
(1)∪(2)=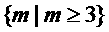 ∪
∪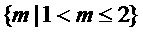
=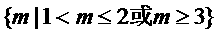
附加题20、(本小题满分10分)
已知三个关于 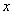 的方程:
的方程:
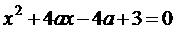 ,
,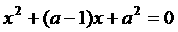 ,
,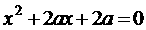 中至少有一个方程有实数根,求实数a的取值范围.
中至少有一个方程有实数根,求实数a的取值范围.
解:设上述三个方程都没有实数根a的取值范围记作集合A,则所求实数a的取值范围为集合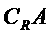 。
。
而三个方程都没有实数根的充要条件是;

解这个不等式组: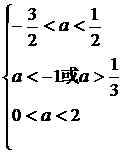 Þ
Þ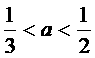
∴A={a|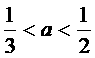 }
}
∴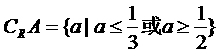
∴三个方程中至少有一个方程有实数根,实数a的取值范围是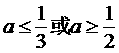 。
。
18、(本小题满分12分)已知集合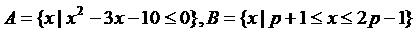 ,若
,若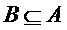 ,求实数p的取值范围。
,求实数p的取值范围。
解:化简集合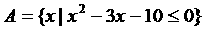
={x|-2<x<5}
∵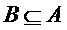
∴(1)B=Æ即: p+1>2p-1
p
<2 时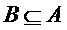 成立.
成立.
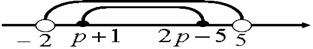
(2) B≠Æ时只须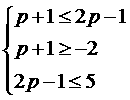
∴2≤p≤3
综上所述p的取值范围是:
{p| p <2或2≤p≤3}={p| p≤3}
17、(本小题满分6+8+10=24分)解关于x的不等式或不等式组:
(1)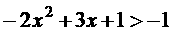
解:整理得: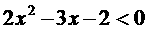
∵方程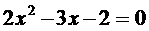 的两根为-1/2、2。
的两根为-1/2、2。
∴不等式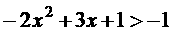 的解集为:{x|-1/2<x<2}
的解集为:{x|-1/2<x<2}
(2) 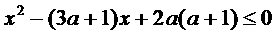
解:∵方程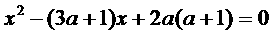
的两根为2a、a+1,
∴① 2a≥a+1即a≥1时,不等式的解集为:
{x| a+1≤x≤2a }
② 2a<a+1即a<1时,不等式的解集为:
{x| 2a≤x≤a+1 }
(3) 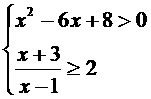 解:解不等式
解:解不等式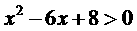 ……(ⅰ)
……(ⅰ)
得:{x|x<2或x>4}
解不等式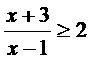 ……(ⅱ)
……(ⅱ)
整理得: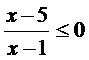 它等价于(Ⅰ)
它等价于(Ⅰ)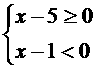 或(Ⅱ)
或(Ⅱ)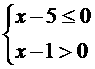
解(Ⅰ)得:x∈Æ;解(Ⅱ) 得:{x|1<x≤5}
∴不等式(ⅱ) 的 解集为(Ⅰ) ∪(Ⅱ)= {x|1<x≤5}
∴不等式的 解集为(ⅰ) ∪(ⅱ)= {x|x<2或x>4}∪{x|1<x<5}={x|1<x<2或4<x≤5}
16、(本小题满分12分)分别写出由下列各命题构成的“p或q”,“p且q”,“非p”形式的复合命题,并判断复合命题的真假:
(1) p:6是12的约数;q:8是12的约数;
(2)菱形的对角线相等;q:菱形的对角线互相垂直平分;
解:(1)“p或q”:6是12的约数或8是12的约数。 真命题
“p且q”:6是12的约数且8是12的约数。 假命题
“非p”:6不是12的约数 假命题
(2)“p或q”:矩形的对角线相等或互相垂直平分。 真命题
“p且q”:矩形的对角线相等且互相垂直平分。 假命题
“非p”:矩形的对角线不相等。 假命题
15、对任意实数x,若不等式|x+1|-|x-2|>k恒成立,则k的取值范围是 k<-3。
14、已知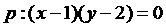 ,
,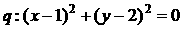 ,则p是q的必要不充分条件.
,则p是q的必要不充分条件.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com