
题目列表(包括答案和解析)
9、若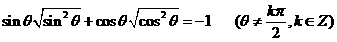 ,则
,则 所在象限是( )
所在象限是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
8、在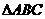 中,“
中,“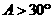 ”是“
”是“ ”的 ( )
”的 ( )
A、仅充分条件 B、仅必要条件 C、充要条件 D、既不充分也不必要条件
7、若 ,则
,则 的值为( )
的值为( )
A、 B、
B、 C、
C、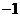 D、
D、
6、若角 的终边过点
的终边过点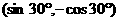 ,则
,则 等于( )
等于( )
A、 B、
B、
 C、
C、
 D、
D、

5、已知 为第一象限角,则
为第一象限角,则 的终边所在的象限是( )
的终边所在的象限是( )
A、第一或第二象限 B、第二或第三象限
C、第一或第三象限 D、第二或第四象限
4、下列命题中的真命题是( )
A、三角形的内角是第一象限角或第二象限角
B、第一象限的角是锐角 C.第二象限的角比第一象限的角大
D、角 是第四象限角的充分条件是
是第四象限角的充分条件是

3、 的值是(
)
的值是(
)
A、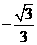 B、
B、 C、
C、 D、
D、
2、在 之间与
之间与 终边相同的角是( )
终边相同的角是( )
A、 B、
B、 C、
C、 D、
D、
1、下列四个角中,① 、②
、② 、③
、③ ④
④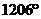 其中是第一象限角的个数是(
)
其中是第一象限角的个数是(
)
A、1个 B、 2个 C、3个 D、4个
24、已知直线l :kx-y+1=0,圆C:x2+y2-4x-5=0,
(1)求证:无论k取任何实数,直线l与圆C恒有两个不同的交点;
(2)当k=2时,直线l与圆C相交于A、B,求A、B两点间的距离;
(3)当实数k变化时,求直线l被圆C截得的弦的中点的轨迹方程.
解:(1)由直线l及圆C的方程消去y可得:(1+k2)x2+(2k-4)x-4=0①,(1¢)
∵D=(2k-4)2+16(1+k2)>0,(2¢)
∴对任意实数k,直线l与圆C有两个不同的交点;(3¢)
(2)经配方得,(x-2)2+y2=9,所以,
圆C的圆心C的坐标是(2,0),半径r=3,所以,当k=2时,
点C到直线l的距离为 ,(5¢)
,(5¢)
故|AB|=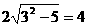 ;(6¢)
;(6¢)
(3)解法一:设两交点A、B的坐标分别为(x1,y1),(x2,y2),A、B的中点P的坐标分别为(x0,y0),(7¢)则
由①可得, ②,(8¢)又由kx0-y0+1=0可得
②,(8¢)又由kx0-y0+1=0可得 ③,(9¢)
③,(9¢)
将③代入②并化简可得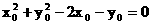 ,
,
故所求的轨迹方程为x2+y2-2x-y=0.(去掉原点)(10¢)
(3)解法二:设两交点A、B的中点P的坐标分别为(x0,y0),(7¢)则
由PC^AB,可得, ②,(8¢)
②,(8¢)
又由kx0-y0+1=0③,(9¢)
将②代入③并化简可得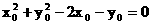 ,
,
故所求的轨迹方程为x2+y2-2x-y=0. (去掉原点)(10¢)
说明:没说明“去掉原点”不扣分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com