
题目列表(包括答案和解析)
20. 如图:在三棱锥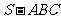 中,已知点
中,已知点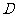 、
、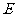 、
、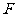 分别为棱
分别为棱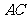 、
、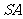 、
、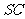 的中点.
的中点.
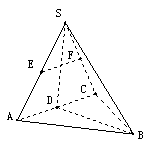 ①求证:
①求证: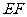 ∥平面
∥平面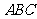 .
.
②若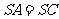 ,
,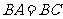 ,求证:平面
,求证:平面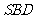 ⊥平面
⊥平面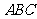 .
.
解:①证明:∵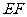 是
是 的中位线,
的中位线,
∴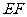 ∥
∥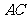 ,
,
又∵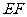
 平面
平面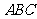 ,
,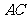
 平面
平面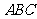 ,
,
∴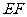 ∥平面
∥平面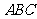 .
.
②证明:∵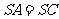 ,
,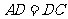
∴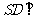
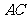 ,
,
∵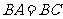 ,
,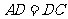
∴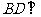
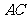 ,
,
又∵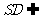 平面
平面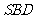 ,
,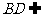 平面
平面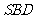 ,
,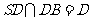 ,
,
∴ 平面
平面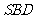 ,
,
又∵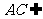 平面
平面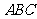 ,
,
∴平面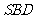 ⊥平面
⊥平面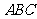 .
.
19. 已知圆心为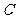 的圆经过点
的圆经过点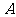 (0,
(0,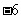 ),
),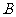 (1,
(1, ),且圆心在直线
),且圆心在直线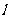 :
: 上,求圆心为
上,求圆心为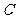 的圆的标准方程.
的圆的标准方程.
解:因为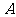 (0,
(0,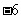 ),
),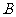 (1,
(1, ),所以线段
),所以线段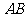 的中点
的中点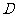 的坐标为
的坐标为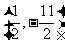 ,
,
直线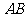 的斜率
的斜率 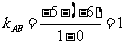 ,
,
因此线段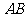 的垂直平分线
的垂直平分线 的方程是
的方程是
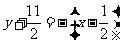 ,
,
即
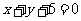
圆心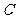 的坐标是方程组
的坐标是方程组 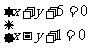 ,的解.
,的解.
解此方程组,得
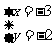 ,
,
所以圆心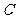 的坐标是(
的坐标是( ,
, ).
).
圆心为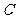 的圆的半径长
的圆的半径长
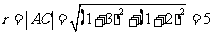
所以,圆心为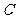 的圆的标准方程是
的圆的标准方程是

18. 求经过两条直线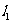 :
: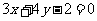 与
与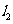 :
: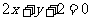 的交点
的交点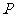 ,且垂直于直线
,且垂直于直线
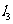 :
: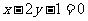 直线
直线 的方程.
的方程.
解:由 解得
解得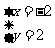
∴ 点P的坐标是( ,2)
,2)
∵ 所求直线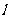 与
与 垂直,
垂直,
∴ 设直线 的方程为
的方程为 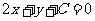
把点P的坐标代入得 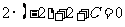 ,得
,得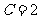
∴ 所求直线 的方程为
的方程为 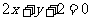
16. 如图,在正方体
如图,在正方体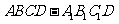 中,异面
中,异面
直线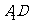 与
与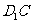 所成的角为_______度;直线
所成的角为_______度;直线
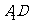 与平面
与平面 所成的角为_______度.
所成的角为_______度. 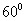 ,
,
三:解答题:
17:设全集U为R,已知A={x|1<x<7},B={x|x<3或x>5},
求(1)A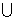 B (2)A
B (2)A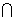 B
(3)(CUA)
B
(3)(CUA)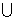 (CUB)
(CUB)
解(1)R ; (2){x|1<x<3或5<x<7}; (3){x|x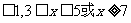 }.
}.
15.  0 ;若
0 ;若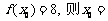 4 .
4 .
14、一个圆柱和一个圆锥的底面直径和他们的高都与某一个球的直径相等,这时
圆柱、圆锥、球的体积之比为 .3:1:2
13、函数y=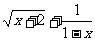 的定义域是
{x|x
的定义域是
{x|x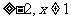 }
}
12、设入射光线沿直线 y=2x+1 射向直线 y=x, 则被y=x 反射后,反射光线所在的
直线方程是( )
A.x-2y-1=0 B.x-2y+1=0 C.3x-2y+1=0 D.x+2y+3=0
11、直线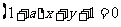 与圆
与圆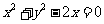 相切,则
相切,则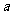 的值为( C ).
的值为( C ).
A. 1,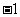 B.
B.  C.
C.
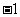 D.
1
D.
1
10、下列命题中错误的是( B ).
A. 若 ,则
,则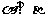 B. 若
B. 若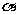
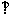
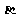 ,
,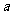

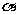 ,则
,则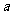
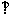
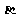
C. 若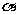
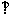
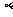 ,
,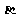
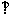
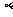 ,
,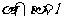 ,则
,则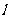
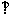
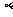
D. 若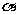
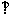
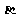 ,
,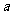
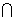
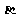 =AB,
=AB,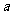 //
//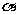 ,
,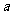
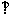 AB,则
AB,则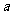
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com