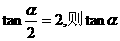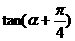12. 已知的值为　　　　　　 ，的值为　　　　　 .

11. ＝___________

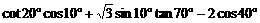24．(本题满分14分)已知函数f (x)＝．

(1)判断f (x)在区间(0，+∞)的单调性，并用定义证明；

(2)写出函数f (x)＝的单调区间．

必修1(A)卷双向细目表　

说明：A：了解 B：理解与掌握C：综合运用

23．(本题满分12分)销售甲、乙两种商品所得利润分别是P(万元)和Q(万元)，它们与投入资金t(万元)的关系有经验公式P＝，Q＝t．今将3万元资金投入经营甲、乙两种商品，其中对甲种商品投资x(万元)．

求：(1)经营甲、乙两种商品的总利润y(万元)关于x的函数表达式；

(2)总利润y的最大值．

22．(本题满分12分)已知函数f(x)＝lg(2+x)，g(x)＝lg(2－x)，设h(x)＝f(x)+g(x)．

(1)求函数h(x)的定义域；

(2)判断函数h(x)的奇偶性，并说明理由．

21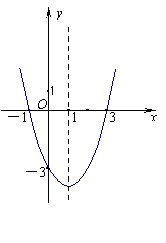．(本题满分12分)已知二次函数的图象如图所示．

(1)写出该函数的零点；

(2)写出该函数的解析式．

20．(本题满分10分)已知U＝R，A＝{x|－1≤x≤3}，B＝{x|x－a＞0}．

(1)若AÍB，求实数a的取值范围；

(2) 若A∩B≠Æ，求实数a的取值范围．

19．(本题满分10分)计算：2log₃2－log₃+log₃8－．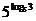

18．在下列从A到B的对应： (1)A＝R，B＝R，对应法则f：x→y＝x² ； (2) A＝R，B＝R，对应法则f：x→y＝； (3)A＝(0，+∞)，B＝{y|y≠0}，对应法则f：x→y＝±；(4)A＝N^*，B＝{－1，1}，对应法则f：x→y＝(－1)^x　 其中是函数的有　　　　　　　 ．(只填写序号)

17．已知2^x+2^－x＝5，则4^x+4^－x的值是　　　　　 ．