
题目列表(包括答案和解析)
2. 求函数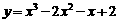 的零点所在区间,并画出它的大致图象.
的零点所在区间,并画出它的大致图象.
(二)、讲授新课:
1、探讨函数零点与方程的根的关系:
① 探讨:方程x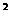 -2x-3=0 的根是什么?函数y= x
-2x-3=0 的根是什么?函数y= x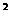 -2x-3的图象与x轴的交点?
-2x-3的图象与x轴的交点?
方程x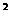 -2x+1=0的根是什么?函数y= x
-2x+1=0的根是什么?函数y= x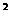 -2x+1的图象与x轴的交点?
-2x+1的图象与x轴的交点?
方程x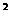 -2x+3=0的根是什么?函数y= x
-2x+3=0的根是什么?函数y= x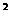 -2x+3的图象与x轴有几个交点?
-2x+3的图象与x轴有几个交点?
② 根据以上探讨,让学生自己归纳并发现得出结论: → 推广到y=f(x)呢?
一元二次方程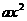 +bx+c=o(a
+bx+c=o(a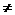 0)的根就是相应二次函数y=ax
0)的根就是相应二次函数y=ax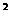 +bx+c的图象与x轴交点横坐标.
+bx+c的图象与x轴交点横坐标.
③ 定义零点:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
④ 讨论:y=f(x)的零点、方程f(x)=0的实数根、函数y=f(x) 的图象与x轴交点的横坐标的关系?
■结论:方程f(x)=0有实数根 函数y=f(x) 的图象与x轴有交点
函数y=f(x) 的图象与x轴有交点 函数y=f(x)有零点
函数y=f(x)有零点
⑤ 练习:求下列函数的零点 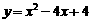 ;
;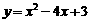 →
→
▲ 小结:二次函数零点情况(由一元二次次方程的判别式去确定)
2、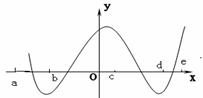 教学零点存在性定理及应用:
教学零点存在性定理及应用:
①、观察下面函数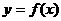 的图象,在区间
的图象,在区间 上______(有/无)零点;
上______(有/无)零点;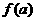 ·
·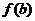 _____0(<或>). 在区间
_____0(<或>). 在区间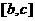 上______(有/无)零点;
上______(有/无)零点;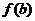 ·
·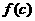 _____0(<或>). 在区间
_____0(<或>). 在区间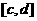 上______(有/无)零点;
上______(有/无)零点;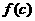 ·
·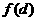 _____0(<或>).
_____0(<或>).
②、◆定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a).f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c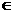 (a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
④ 应用:书本例题1:(P88)求函数f(x)=Lnx+2x-6的零点的个数.(注意:如何证明该函数是严格的单调递增函数?) (试讨论一些函数值→分别用代数法、几何法)
⑤小结:函数零点的求法
■★代数法:求方程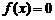 的实数根;
的实数根;
■★几何法:对于不能用求根公式的方程,可以将它与函数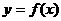 的图象联系起来,并利用函数的性质找出零点.
的图象联系起来,并利用函数的性质找出零点.
⑥ 练习:求函数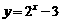 的零点所在区间.
的零点所在区间.
3、小结:零点概念;零点、与x轴交点、方程的根的关系;零点存在性定理
(一)、复习准备:
※★思考:一元二次方程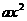 +bx+c=o(a
+bx+c=o(a 0)的根与二次函数y=ax
0)的根与二次函数y=ax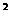 +bx+c的图象之间有什么关系?
+bx+c的图象之间有什么关系?
结合二次函数的图象,判断一元二次方程根的存在性及根的个数,从而了解函数的零点与方程根的联系;掌握零点存在的判定条件.
20.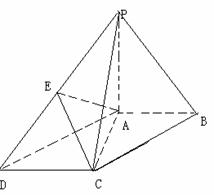 (15分)如图,在底面为平行四边形的四棱锥
(15分)如图,在底面为平行四边形的四棱锥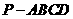 中,
中,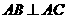 ,
,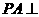 平面
平面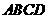 ,且
,且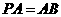 ,点
,点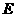 是
是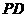 的中点.
的中点.
(Ⅰ)求证: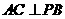 ;(5分)
;(5分)
(Ⅱ)求证: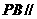 平面
平面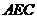 ;(5分)
;(5分)
(Ⅲ)求二面角 的大小.(5分)
的大小.(5分)
21(14分)、猎豹汽车制造厂有一条价值为a万元的汽车生产线,现在要通过技术改造来提高该生产线的生产能力,提高产品的增加值。经市场调查,产品的增加值y万元与技术改造投入x万元之间满足:(1)、y与(a-x)和x的乘积成正比;(2)、当x= 时,y=a2。
又技术改造投入比率为:∈(0,t],其中t是常数,且t∈(0,2]。
(1)、设y=f(x),求函数y=f(x)的表达式(5分)以及定义域(3分);
(2)、求出产品的增加值y的最大值及相应的x之值(6分)。
19.(本题满分12分):已知函数f(x)=2x - ;
(1)、求证:函数f(x)在(-1,+∞)上为增函数;(6分)
(2)、求证:函数f(x)在(0,1)内必有零点。(6分)
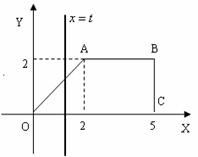
18.(12分)如图,直角梯形OABC位于直线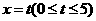 右侧的图形面积为
右侧的图形面积为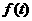 。(1)试求函数
。(1)试求函数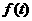 的解析式(8分);
的解析式(8分);
(2)画出函数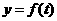 的图象(4分)。
的图象(4分)。
17.(12分)已知ABCD为矩形,E为半圆CED上一点,且平面ABCD⊥平面CDE.
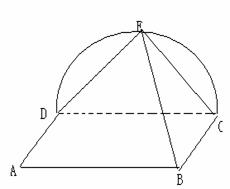 (1)求证:DE是AD与BE的公垂线(6分);
(1)求证:DE是AD与BE的公垂线(6分);
(2)若AD=DE=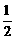 AB,求AD和BE所成的角的大小(6分).
AB,求AD和BE所成的角的大小(6分).
16. (10分)“菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂,如果烟花距地面高度h 米与时间t 秒之间的关系为
(10分)“菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂,如果烟花距地面高度h 米与时间t 秒之间的关系为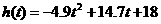 ,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1米)?
,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1米)?
(二)、填空题答案: 11题.__________________; 12题 :_____________; 13题:__________________; 14题:__________________; 15题:________;________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com