
题目列表(包括答案和解析)
★9.函数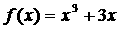 在R上的零点有_____1个
在R上的零点有_____1个
★10.已知函数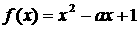 ,若f(x)在R上有一个零点,a=__±2_____;若f(x)在R 上有2个零点,则a的取值范围为________{a|a>2或a<-2}______.
,若f(x)在R上有一个零点,a=__±2_____;若f(x)在R 上有2个零点,则a的取值范围为________{a|a>2或a<-2}______.
★11.方程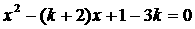 有两个不等实根
有两个不等实根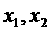 ,且
,且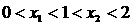 ,则实数k的取值范围为_______(0,
,则实数k的取值范围为_______(0,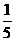 );__.
);__.
★12.若函数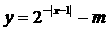 有零点,则实数m的取值范围是____(0,1);_______.
有零点,则实数m的取值范围是____(0,1);_______.
★13.已知函数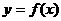 是R上的奇函数,则函数
是R上的奇函数,则函数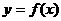 的图象关于___原点____对称; 若
的图象关于___原点____对称; 若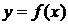 有2005个零点(记为
有2005个零点(记为 ),则
),则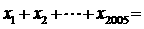 ___0_.
___0_.
★1. 函数 的零点为 ( A )
的零点为 ( A )
(A).1或3 (B).-1或3 (C).1或-3 (D).-1或-3
★2. 下列函数在区间[1,2]上有零点的是 ( D )
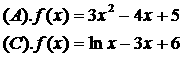
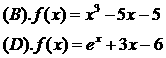
★3. 下列函数中有两个零点的是 ( D )
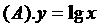
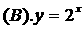
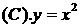
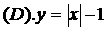
★4. 方程 的根的个数为 ( B )
的根的个数为 ( B )
(A).0 (B).1 (C).2 (D).3
★5. 方程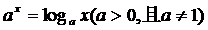 的解的个数是 ( D )
的解的个数是 ( D )
(A).0 (B).1 (C).2 (D).与a的取值有关
★6. 下列函数图象与x轴均有交点,其中不能用二分法求图中交点的横坐标的是( A )
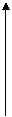
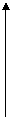
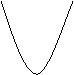 y
y
y
y
y
y
y
y


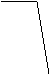




 0 1
2 3 x 0 1 x 0 1 x
0 1 2 x
0 1
2 3 x 0 1 x 0 1 x
0 1 2 x
(A)
 (B)
(C)
(D)
(B)
(C)
(D)
★7. 函数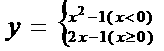 的零点为 ( C )
的零点为 ( C )
(A).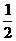 (B).
(B).
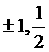 (C).
(C). 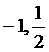 (D).
(D). 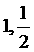
★8.如果函数 在区间(-1,0)内存在零点,则a的取值可以是 ( D )
在区间(-1,0)内存在零点,则a的取值可以是 ( D )
(A)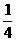 (B)0
(C)
(B)0
(C) 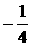 (D) –1
(D) –1
(四).课堂回顾与小结:
二分法的概念, 二分法的步骤;注重二分法思想
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义二十:函数与方程复习 ---- 《函数与方程》同步练习
撰稿: 方锦昌 电子邮箱 fangjingchang2007@ 手机号码 13975987411
(三)、巩固练习:
★1、 设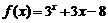 , 用二分法求方程
, 用二分法求方程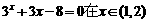 内近似解的过程中, 计算得到
内近似解的过程中, 计算得到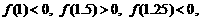 则方程的根落在区间( B ).
则方程的根落在区间( B ).
A.(1,1.25) B.(1.25,1.5) C.(1.5,2) D.不能确定
★2.(2005年北京高考第20题·14分)
设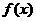 是定义在[0,1]上的函数,若存在x*
是定义在[0,1]上的函数,若存在x* 上单调递增,在[x*,1]上单调递减,则称
上单调递增,在[x*,1]上单调递减,则称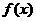 为[0,1]上的单峰函数, x*为峰点,包含峰点的区间为含峰区间.
为[0,1]上的单峰函数, x*为峰点,包含峰点的区间为含峰区间.
对任意的[0,1]上的单峰函数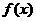 ,下面研究缩短其含峰区间长度的方法.
,下面研究缩短其含峰区间长度的方法.
(Ⅰ)证明:对任意的 为含峰区间;
为含峰区间;
若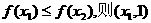 为含峰区间;
为含峰区间;
(Ⅱ)对给定的r(0<r<0.5),证明:存在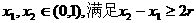 ,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;
,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;
(Ⅲ)选取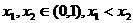 ,由(Ⅰ)可确定含峰区间为(0,
,由(Ⅰ)可确定含峰区间为(0,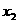 )或(
)或(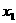 ,1),在所得的含峰区间内选取
,1),在所得的含峰区间内选取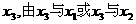 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,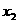 )的情况下,试确定
)的情况下,试确定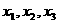 的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34. (区间长度等于区间的右端点与左端点之差)
的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34. (区间长度等于区间的右端点与左端点之差)
●解:(I)证明:设x*为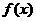 的峰点,则由单峰函数定义可知
的峰点,则由单峰函数定义可知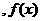 在
在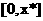 上单调递增,
上单调递增,
在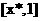 上单调递减. 当
上单调递减. 当 时,假设
时,假设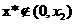 ,则
,则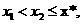 从而
从而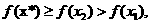 这与
这与 矛盾,所以
矛盾,所以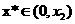 ,即
,即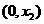 是含峰区间.
是含峰区间.
当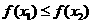 时,假设
时,假设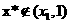 ,则
,则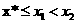 ,从而
,从而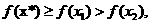 这与
这与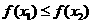 矛盾,所以
矛盾,所以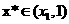 ,即
,即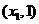 是含峰区间.
是含峰区间.
(II)证明:由(I)的结论可知: 当 时,含峰区间的长度为
时,含峰区间的长度为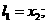 当
当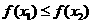 时,含峰区间的长度为
时,含峰区间的长度为 对于上述两种情况,由题意得
对于上述两种情况,由题意得
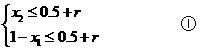
由①得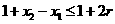 ,即
,即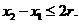
又因为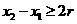 ,所以
,所以 ;
;
将②代入①得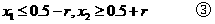 ;
;
由①和③解得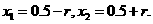 所以这时含峰区间的长度
所以这时含峰区间的长度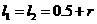 ,即存在
,即存在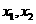 使得所确定的含峰区间的长度不大于
使得所确定的含峰区间的长度不大于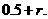
(III)解:对先选择的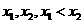 ,由(II)可知
,由(II)可知
在第一次确定的含峰区间为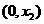 的情况下,
的情况下, 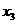 的取值应满足
的取值应满足
由④与⑤可得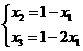 当
当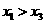 时,含峰区间的长度为
时,含峰区间的长度为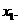 由条件
由条件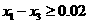 ,得
,得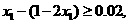 ,从而
,从而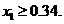
因此,为了将含峰区间的长度缩短到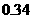 ,只要取
,只要取 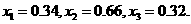
(二)、讲授新课:
1. 教学二分法的思想及步骤:
★① 出示例:有12个小球,质量均匀,只有一个是比别的球重的,你用天平称几次可以找出这个球的,要求次数越少越好. ( 让同学们自由发言,找出最好的办法)
◆解:第一次,两端各放六个球,低的那一端一定有重球;第二次,两端各放三个球,低的那一端一定有重球;第三次,两端各放一个球,如果平衡,剩下的就是重球,否则,低的就是重球.
其实这就是一种二分法的思想,那什么叫二分法呢?
② 探究: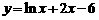 的零点所在区间?如何找出这个零点? → 师生用二分法探索
的零点所在区间?如何找出这个零点? → 师生用二分法探索
③ 定义二分法的概念:对于在区间[a,b]上连续不断且f(a).f(b)<0的函数y=f(x),通过不断的把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法(bisection)
④ 探究:给定精度ε,用二分法求函数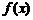 的零点近似值的步骤如下:
的零点近似值的步骤如下:
A.确定区间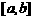 ,验证
,验证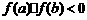 ,给定精度ε;B. 求区间
,给定精度ε;B. 求区间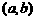 的中点
的中点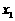 ;
;
C. 计算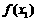 : 若
: 若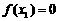 ,则
,则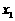 就是函数的零点; 若
就是函数的零点; 若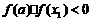 ,则令
,则令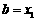 (此时零点
(此时零点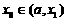 ); 若
); 若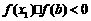 ,则令
,则令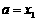 (此时零点
(此时零点 );
);
D. 判断是否达到精度ε;即若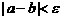 ,则得到零点值a(或b);否则重复步骤2-4.
,则得到零点值a(或b);否则重复步骤2-4.
2. 教学例题:
① 出示例:借助计算器或计算机用二分法求方程2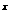 +3x=7的近似解. (师生共练)
+3x=7的近似解. (师生共练)
② 练习:求函数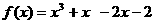 的一个正数零点(精确到
的一个正数零点(精确到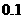 )
)
(一)、复习准备:
★1. 提问:什么叫零点?零点的等价性? 零点存在性定理?
零点概念:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
方程f(x)=0有实数根 函数y=f(x) 的图象与x轴有交点
函数y=f(x) 的图象与x轴有交点 函数y=f(x)有零点
函数y=f(x)有零点
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a).f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c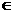 (a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
★2. 探究:一元二次方程求根公式? 三次方程? 四次方程?
材料:高次多项式方程公式解的探索史料:在十六世纪,已找到了三次和四次函数的求根公式,但对于高于4次的函数,类似的努力却一直没有成功,到了十九世纪,根据阿贝尔(Abel)和伽罗瓦(Galois)的研究,人们认识到高于4次的代数方程不存在求根公式,亦即,不存在用四则运算及根号表示的一般的公式解.同时,即使对于3次和4次的代数方程,其公式解的表示也相当复杂,一般来讲并不适宜作具体计算.因此对于高次多项式函数及其它的一些函数,有必要寻求其零点的近似解的方法,这是一个在计算数学中十分重要的课题
★3、生活实例:
●高沙至洞口的一条电话线路发生故障,请问如何去迅速查出故障之所在?
 ▲解:如果沿着线路一小段一小段去查找,困难很多;每查一次要爬一次电杆,10KM长的线路,大约有200多根电杆。
▲解:如果沿着线路一小段一小段去查找,困难很多;每查一次要爬一次电杆,10KM长的线路,大约有200多根电杆。
维修人员这样工作最合理:
①、先从中间位置板桥查起:若用随身所带的话机向两端测试,发现高沙到板桥段正常,则可确定板桥到洞口段有故障;
②、再从中间位置花古处查,若板桥到花古段正常,则可确定故障出花古到洞口段。------每查一次,则可将线路缩短一半,当把故障可能发生的范围缩小到50m-100m左右时,即只有一至两根电线杆时,则只要查几次就够了。----这种检查线路故障的方法,不仅可用于查找线路、水管、气管等故障,还能用于实验设计、资料查询等,同时也是本节所学的求方程的近似解的二分法方法。
●1、判断方程在区间(,8)上是否存在有实数解,并说明理由:log2x+3x-2=0
★解:∵f()<0,f(8)>0,且f(x)连续,则方程有实数解。)
●2、若方程ax2-x-1=0在(0,1)内有解,则实数a的取值范围是_____
★解:f(0)¦(1)<0,则a>2
●3、方程lgx+x=0的根所在区间是( B )
A (-∞,0) B (0,1) C (1,2) D (2,4)
●4、若函数¦(x)=x2-ax-b的两个零点是2和3,则函数g(x)=bx2-ax-1的零点是______,
● 5、已知二次函数¦(x)=x2-(m-1)x+2m在区间[0,1]上有且只有一个零点,求实数m的取值范围
★解:[-2,0])
●6.设函数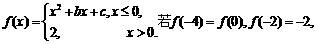 则关于x的方程
则关于x的方程
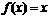 解的个数为( C )
解的个数为( C )
A.1 B.2 C.3 D.4
● 7、使log2(-x)<x+1成立的x的取值范围是_____(-1,0)
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十九:用二分法求方程的近似解
撰稿: 方锦昌 电子邮箱 fangjingchang2 007@ 手机号码 13975987411
5. 作业:P92, 2题;P93: 3题
4. 已知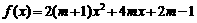 :
:
(1) 为何值时,函数的图象与
为何值时,函数的图象与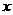 轴有两个零点;
轴有两个零点;
(2)如果函数至少有一个零点在原点右侧,求 的值.
的值.
3. 求下列函数的零点:① 、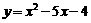 ; ②、
; ②、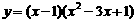 ;
;
③、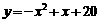 ; ④、
; ④、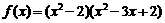 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com