(一)、新课引入：前节课主要是讲授指数函数、对数函数以及幂函数的增长差异，本节课我们主要是通过一些生活中常遇到的实例来进一步说明函数模型在解决实际问题中的应用.

(四)、常见的函数模型：

①、一次函数型模型：y=kx+b(k、b为常数，且k≠0)

②、二次函数型模型：y=ax²+bx+c(a、b、c为常数，且a≠0)

③、指数函数型模型：y=ab^x+c(a、b、c为常数，且a≠0，b>0，b≠1)

④、对数函数型模型：y=mlog_a^x+n(m、n、a为常数，且a>0，a≠1)

⑤、幂函数型模型：y=axⁿ+b(a、b、n为常数，且a≠0，n≠1)

湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义

　　　　　 讲义二十二：几类不同增长的函数模型(2)　　

撰稿： 方锦昌　 电子邮箱 fangjingchang2 007@　　 手机号码 13975987411

(三)、巩固练习：

★1、令人目瞪口呆的“指数爆炸”：

王先生从今天开始每天给你10万元，而你则第一天给王先生1元，第二天给王先生2元，第三天给王先生4元，第四天给王先生8元……第n天给王先生2^n-1元；

①、若王先生要与你签订15天的合同，你同意吗？

②、若王先生要与你签订30天的合同，你认为怎样呢？(可用公式有：2⁰+2¹+2²+2³+2⁴+…+2^n-1=)

◆解：①、S₁=2¹⁵-1=32767(元)< 150(万元)，可以接受；

②、S₂=2³⁰-1=1073741823(元)>300(万元)，无法接受。

★2、以下四种说法中，正确的是(　 D )

A、对任意的x>0，x^a>log_a^x(0<a<1)　　 B、对任意的x>0，x^a>log_a^x(a>1)

C、对任意的x>0，a^x>log_a^x　　　　　 D、一定存在有x₀，使得当x>x₀时，总有a^x>xⁿ>log_a^x成立。

(二)、讲授新课：

1、例题讲解：

★① 书本P95面例1．假设你有一笔资金用于投资，现有三种投资方案供你选择，这三种方案的回报如下：方案一：每天回报40元；

方案二：第一天回报10元，以后每天比前一天多回报10元；

方案三：第一天回报0 .4元，以后每天的回报比前一天翻一番．请问，你会选择哪种投资方案？

② 探究：在本例中涉及哪些数量关系？如何用函数描述这些数量关系？→师生共同分析解答

探究：根据例1的数据，你对三种方案分别表现出的回报资金的增长差异有什么认识？

借助计算器或计算机作出函数图象，并通过图象描述一下三种方案的特点吗？

根据以上分析，你认为就作出如何选择？

★③书本P97： 例2. 某公司为了实现1000万元利润的目标，准备制定一个激励销售部门的奖励方案：在销售利润达到10万元时，按销售利润进行奖励，且奖金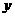(单位：万元)随销售利润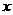(单位：万元)的增加而增加但奖金不超过5万元，同时奖金不超过利润的25%．现有三个奖励模型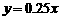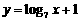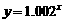：；；. 问：其中哪个模型能符合公司的要求？

④ 探究：本例涉及了哪几类函数模型？本例的实质是什么？

根据问题中的数据，如何判定所给的奖励模型是否符合公司要求？

通过对三个函数模型增长差异的比较，写出例2的解答．

2、探究与发现： 幂函数、指数函数、对数函数的增长差异分析：当自变量变得很大时，指数函数比一次函数增长得快，一次函数比对数函数增长得快。

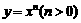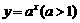你能否仿照前面例题使用的方法，探索研究幂函数、指数函数、对数函数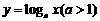在区间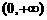上的增长差异：

在区间(0，+∞)上，尽管函数y=a^x(a>1)、y=log_a^x(a>1)、y=xⁿ(n>0)都是增函数，但它们的增长速度是不相同的，而且不在同一个“档次”上。随着x的增大，y=a^x(a>1)的增长速度会越来越快，会超过并远远大于y=xⁿ(n>0)的增长速度，而y=log_a^x(a>1)的增长速度则会越来越慢，因此总会存在一个x₀，当x>x₀时，就有log_a^x<xⁿ<a^x。

3、尝试练习： 教材P₁₁₀练习1、2； 教材P₁₁₃练习．

4、小结与反思：直线上升、指数爆炸、对数增长等不同函数模型的增长的含义；数学的实用性

(一)、新课引入：

国际象棋棋盘的奖赏→教科书第三章的章头图：澳大利亚兔子数“爆炸”。

有一大群喝水、嬉戏的兔子，但是这群兔子曾使澳大利亚伤透了脑筋．1859年，有人从欧洲带进澳洲几只兔子，由于澳洲有茂盛的牧草，而且没有兔子的天敌，兔子数量不断增加，不到100年，兔子们占领了整个澳大利亚，数量达到75亿只．可爱的兔子变得可恶起来，75亿只兔子吃掉了相当于75亿只羊所吃的牧草，草原的载畜率大大降低，而牛羊是澳大利亚的主要牲口．这使澳大利亚头痛不已，他们采用各种方法消灭这些兔子，直至二十世纪五十年代，科学家采用载液瘤病毒杀死了百分之九十的野兔，澳大利亚人才算松了一口气．

将实际问题转化为函数模型，比较常数函数、一次函数、指数函数、对数函数模型的增长差异，结合实例体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义．

①、结合实例体会直线上升，指数爆炸，对数增长等不同增长的函数模型的意义.

②、借助信息技术，利用函数图象及数据表格，比较指数函数、对数函数以及幂函数的增长差异.

③、恰当运用函数的三种表示法(解析式、图象、表格)并借助信息技术解决一些实际问题.

④、收集一些社会生活中普遍使用的函数模型(指数函数、对数函数、幂函数、分段函数等)，了解函数模型的广泛应用.

★14. 已知函数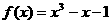,判断方程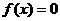在区间[1,1.5]内是否有实数解,如果有,求出一个近似解(精确到0.1). (答案为1.3)

★15.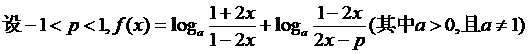

(1)　　 求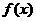的定义域;(2)、求证:函数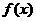无零点.

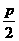●解：(1){x|<x<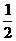}；　 (2)反证法.

湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义

　　　　　　　 讲义二十一：几类不同增长的函数模型及时其应用(1)　　

撰稿： 方锦昌　 电子邮箱 fangjingchang2 007@　　 手机号码 13975987411