
题目列表(包括答案和解析)
9. 若||=,||=2,且(-)⊥,则与的夹角是
A. B. C. D.
8. 设F(x)= f (x)+
f (-x),x∈R,[-π,-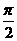 ]是函数F(x)的单调递增区间,将F(x)的图象按向量a=(π,0)平移得到一个新的函数G(x)的图象,则G(x)的单调递减区间必是
]是函数F(x)的单调递增区间,将F(x)的图象按向量a=(π,0)平移得到一个新的函数G(x)的图象,则G(x)的单调递减区间必是
A.[-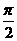 ,0]
B.[
,0]
B.[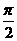 ,π] C.[π,
,π] C.[π,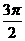 ]
D.[
]
D.[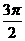 ,2π]
,2π]
7. 已知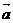 ,
,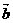 是两个相互垂直的单位向量,而
是两个相互垂直的单位向量,而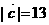 ,
,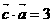 ,
, 。则对于任意实数
。则对于任意实数 ,
, 的最小值是
的最小值是
A.5 B.7 C.12 D.13
6. 若非零向量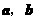 满足
满足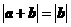 ,则
,则
A.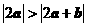 B.
B.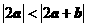
C.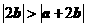 D.
D. 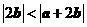
5. 有下面四个命题:
①“x=2kπ+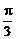 (k∈Z)”是“tanx=
(k∈Z)”是“tanx=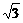 ”的充分不必要条件;
”的充分不必要条件;
②函数f(x)=|2cosx-1|的最小正周期是π;
③函数f(x)=sin(x+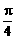 )在[
)在[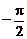 ,
,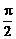 ]上是增函数;
]上是增函数;
④若函数f(x)=asinx-bcosx的图象的一条对称轴的方程为x=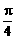 ,则a+b=0.
,则a+b=0.
其中正确命题的个数是
A.1 B.2 C.3 D.4
4. 设集合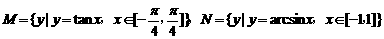 ,则
,则
A. 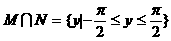 B.
B. 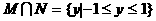
C. 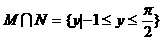 D.
D. 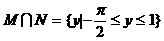
3. 函数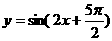 的图象的一条对称轴方程是
的图象的一条对称轴方程是
A.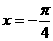 B.
B.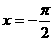 C.
C. D.
D.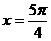
2. 下列函数中,周期为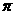 的奇函数是
的奇函数是
A.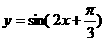 B.
B. 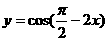 C. y=|sinx| D. y=tan2x
C. y=|sinx| D. y=tan2x
1. 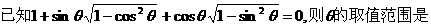
A.第三象限角。 B.第四象限角。
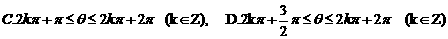
(四)补充例题:
★[例题]某飞机制造公司一年中最多可生产某种型号的飞机100架。已知制造x架该种飞机的产值函数为R(x)=3000x-20x2 (单位:万元),成本函数
C(x)=500x+4000 (单位:万元)。利润是收入与成本之差,又在经济学中,函数¦(x)的边际利润函数M¦x)定义为:M¦x)=¦(x+1)-¦(x).
①、求利润函数P(x)及边际利润函数MP(x);(利润=产值-成本)
②、问该公司的利润函数P(x)与边际利润函数MP(x)是否具有相等的最大值?
●解:①P(x)= R(x)- C(x)= -20x2+2500x-4000 (x∈N*,且x∈[1,100]);
MP(x)= P(x+1)- P(x)=-40x+2480(x∈N*,且x∈[1,100]);
②P(x)= -20(x-)2+74125 (x∈N*,且x∈[1,100]);则当x=62或63时,P(x)max=74120(元),因为MP(x) =-40x+2480为↘,则当x=1时,MP(x)max =2440元,故利润函数与边际利润函数不具有相等的最大值。
★[例题2]. (湖南2006年高考理科20题14分)对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为: )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为
)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为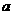 (1≤a≤3).设用
(1≤a≤3).设用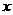 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是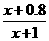 (
( ),用
),用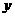 质量的水第二次清洗后的清洁度是
质量的水第二次清洗后的清洁度是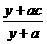 ,其中
,其中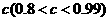 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度.
(Ⅰ)分别求出方案甲以及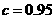 时方案乙的用水量,并比较哪一种方案用水量较少;
时方案乙的用水量,并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙,当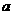 为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论
为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论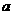 取不同数值时对最少总用水量多少的影响.
取不同数值时对最少总用水量多少的影响.
解:(Ⅰ)设方案甲与方案乙的用水量分别为x与z,由题设有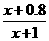 =0.99,解得x=19. 由
=0.99,解得x=19. 由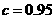 得方案乙初次用水量为3, 第二次用水量y满足方程:
得方案乙初次用水量为3, 第二次用水量y满足方程: 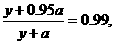 解得y=4
解得y=4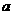 ,故z=4
,故z=4 +3.即两种方案的用水量分别为19与4
+3.即两种方案的用水量分别为19与4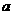 +3.因为当
+3.因为当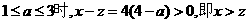 ,故方案乙的用水量较少.(II)设初次与第二次清洗的用水量分别为
,故方案乙的用水量较少.(II)设初次与第二次清洗的用水量分别为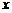 与
与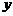 ,类似(I)得
,类似(I)得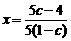 ,
,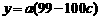 (*)于是
(*)于是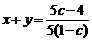 +
+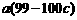
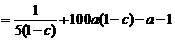 ;当
;当 为定值时,
为定值时,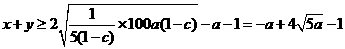 , 当且仅当
, 当且仅当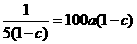 时等号成立.此时
时等号成立.此时 将
将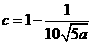 代入(*)式得
代入(*)式得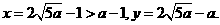 故
故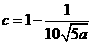 时总用水量最少, 此时第一次与第二次用水量分别为
时总用水量最少, 此时第一次与第二次用水量分别为 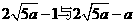 , 最少总用水量是
, 最少总用水量是 .
当
.
当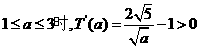 ,故T(
,故T(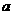 )是增函数(也可以用二次函数的单调性判断).这说明,随着
)是增函数(也可以用二次函数的单调性判断).这说明,随着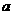 的值的最少总用水量, 最少总用水量最少总用水量.
的值的最少总用水量, 最少总用水量最少总用水量.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com