17．△ABC中，D在边BC上，且BD＝2，DC＝1，∠B＝60^o，∠ADC＝150^o，求AC的长及△ABC的面积．

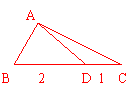在△ABC中，∠BAD＝150^o－60^o＝90^o，∴AD＝2sin60^o＝．

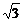在△ACD中，AD²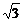＝()²+1²－2×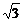×1×cos150^o＝7，∴AC＝．

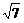∴AB＝2cos60^o＝1．S_△ABC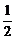＝×1×3×sin60^o＝．

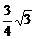16．数列通项公式为a_n＝n²－5n+4，问

(1)数列中有多少项是负数？(2)n为何值时，a_n有最小值？并求出最小值.

(1)由a_n为负数，得n²－5n+4<0，解得1<n<4.

∵n∈N^*，故n＝2或3，即数列有2项为负数，分别是第2项和第3项.

(2)∵a_n＝n²－5n+4＝(n－)²－，∴对称轴为n＝＝2.5

又∵n∈N^*，故当n＝2或n＝3时，a_n有最小值，最小值为2²－5×2+4＝－2.

15．已知三个数成等差数列，其和为15，其平方和为83，求此三个数.

解：设此三数分别为x－d、x、x+d

则

解得x＝5，d＝±2.

∴所求三个数列分别为3、5、7或7、5、3.

14．已知数列{a_n}为等差数列，a₃＝，a₇＝－，求a₁₅的值.

利用通项公式，设数列{a_n}的首项为a₁,公差为d

则　　解之得

a₁₅＝a₁+14d＝+14×(－)＝－

13．若三角形中有一个角为60°，夹这个角的两边的边长分别是8和5，则它的内切圆半径等于________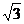　 外接圆半径等于________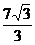

　分析：设60°的角的对边长为x，外接圆半径为R，内切圆半径为r，则x²＝8²+5²-2×8×5×cos60°＝49，∴　x＝7

　∵　7＝2Rsin60°，∴　R＝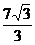

　∵　S_△ABC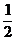＝×8×5×sin60°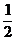＝×r×(8+5+7)，∴　r＝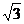

12．已知f(n+1)＝f(n)－(n∈N^*)且f(2)＝2，则f(101)＝_______－　

11．在△ABC中，a、b、c分别为A、B、C的对边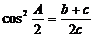，，则△ABC的形状为______直角三角形

10．在△ABC中，若AB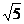＝，AC＝5，且cosC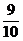＝，则BC＝__________4或5　　　

9．已知△ABC的面积为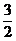，且b＝2，c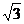＝，则∠A＝__________60°或120°

8．在△ABC中，若b＝2csinB，则∠C＝________30°或150°