
题目列表(包括答案和解析)
1. 练习:课本64页练习1、2、3、4题
(二)、讲授新课:
1. 教学对数的概念:
① 定义:一般地,如果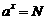
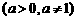 ,那么数 x叫做以a为底 N的对数(logarithm).
,那么数 x叫做以a为底 N的对数(logarithm).
记作 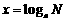 ,其中a叫做对数的底数,N叫做真数
,其中a叫做对数的底数,N叫做真数
② 定义:我们通常将以10为底的对数叫做常用对数(common logarithm),并把常用对数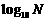 简记为lgN
简记为lgN 在科学技术中常使用以无理数e=2.71828……为底的对数,以e为底的对数叫自然对数,并把自然对数
在科学技术中常使用以无理数e=2.71828……为底的对数,以e为底的对数叫自然对数,并把自然对数 简记作lnN
简记作lnN → 认识:lg5 ; lg3.5; ln10; ln3
→ 认识:lg5 ; lg3.5; ln10; ln3
③ 讨论:指数与对数间的关系 (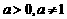 时,
时,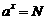

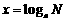 )
)
|
式子 名称 |
a |
b |
N |
|
指数式ab=N |
底数 |
指数 |
幂 |
|
对数式logaN=b |
底数 |
对数 |
真数 |
负数与零是否有对数? (原因:在指数式中
N
> 0 )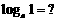 ,
, 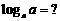
2. 教学指数式与对数式的互化:
★① 出示P63:例1. 将下列指数式写成对数式: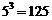 ;
;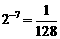 ;
;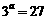 ;
; 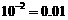
★② 出示例2. 将下列对数式写成指数式: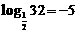 ; lg0.001=-3; ln100=4.606
; lg0.001=-3; ln100=4.606
(学生试练 → 订正 →
变式: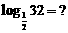 lg0.001=? )
lg0.001=? )
★③ 出示例3. 求下列各式中x的值:
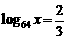 ;
; 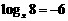 ;
; 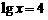 ;
; 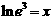
(讨论:解方程的依据? → 试求 → 小结:应用指对互化求x)
★④
练习:求下列各式的值: 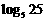 ;
;
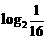 ;
;
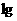 10000
10000
★⑤ 探究: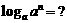
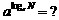
3. 小结:对数概念;lgN与lnN;指数与对数的互化; 如何求对数值
(一)、复习准备:
★1.问题1:庄子:一尺之棰,日取其半,万世不竭 (1)取4次,还有多长?(2)取多少次,还有0.125尺?
(得到:
(1)取4次,还有多长?(2)取多少次,还有0.125尺?
(得到: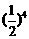 =?,
=?,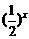 =0.125
=0.125 x=?)
x=?)
★2.问题2:假设2002年我国国民生产总值为a亿元,如果每年平均增长8%,那么经过多少年国民生产 是2002年的2倍? ( 得到: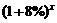 =2
=2 x=? )
x=? )
▲问题共性:已知底数和幂的值,求指数 怎样求呢?例如:课本实例由
怎样求呢?例如:课本实例由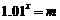 求x
求x
(五)、. 教学指数形式的函数定义域、值域:
◆1、①设y1=40.9,y2=80.48;y3=()-1.5,则三者的大小是_____y1>y3>y2
②设函数F(x)=[1+]·f(x)(且x≠0)是偶函数,又f(x)不恒等于0,则f(x)的奇偶性是_
(答案为:奇函数); ③函数y=1-2x,x∈[1,4]的值域为____[-15,-1]; ④、函数f(x)=()x+2,x∈[-1,2]的值域为____[,5];⑤函数y=a-x(a>0,a≠1)当a∈______时,它为↘ ,此时,当x∈___时,y<0 .答案:(1,+∞)Æ
⑥、已知函数f(x)=的定义域为(-∞,0)则a的取值范围是____(答案:0<a<1)
▲2.①、 一片树林中现有木材30000m3,如果每年增长5%,经过x年树林中有木材ym3,写出x,y间的函数关系式,并利用图象求约经过多少年,木材可以增加到40000m3
 ▲②、. 比较下列各组数的大小:
▲②、. 比较下列各组数的大小: 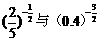 ;
; 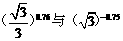 .
.
▲3. 求函数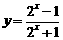 的定义域和值域,并讨论函数的单调性、奇偶性.
的定义域和值域,并讨论函数的单调性、奇偶性.
[★题4]设a>1为常数,已知当x∈(-1,1)时,不等式x2-ax<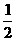 恒成立,则a的取值范围为( A )
恒成立,则a的取值范围为( A )
A (1,2] B [2,+∞) C (1,4] D [4,+∞)
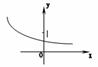
[★题5]已知函数¦(x)=ax –b的图象如图所示,其中a,b为常数,则下列结论正确的是( B )
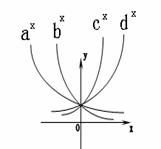 A a>1 b<0 B 0<a<1 b<0 C
a>1 b>0 D 0<a<1,b>0
A a>1 b<0 B 0<a<1 b<0 C
a>1 b>0 D 0<a<1,b>0
[★题6]指数函数y=ax,y=bx,y=cx,y=dx 在同一坐标系中的图象如下图所示,则a、b、c、d的大小顺序为( A )
A b<a<d<c B a<b<d<c C b<a<c<d D b<c<a<d
★[题7]已知实数a, b满足等式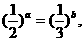 下列五个关系式
下列五个关系式
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有( B ) A.1个 B.2个 C.3个 D.4个
●[解答]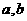 均大于零时,要满足等式,必有
均大于零时,要满足等式,必有 ;
;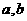 均小于零时,要满足等式,必有
均小于零时,要满足等式,必有 ;
;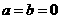 时,显然等式成立.因此不可能成立的关系式为③④,选B
时,显然等式成立.因此不可能成立的关系式为③④,选B
★[题8]设函数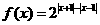 ,求使
,求使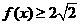 的
的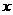 取值范围.答案:
取值范围.答案: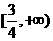
★9.(天津卷)如果函数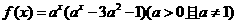 在区间
在区间 上是增函数,那么实数
上是增函数,那么实数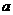 的取值范围是( )A.
的取值范围是( )A.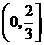 B.
B.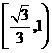 C.
C.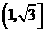 D.
D.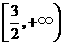
●解析:函数y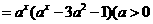 且
且 可以看作是关于
可以看作是关于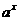 的二次函数,若a>1,则
的二次函数,若a>1,则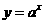 是增函数,原函数在区间
是增函数,原函数在区间 上是增函数,则要求对称轴
上是增函数,则要求对称轴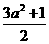 ≤0,矛盾;若0<a<1,则
≤0,矛盾;若0<a<1,则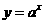 是减函数,原函数在区间
是减函数,原函数在区间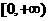 上是增函数,则要求当
上是增函数,则要求当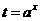 (0<t<1)时,
(0<t<1)时,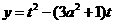 在t∈(0,1)上为减函数,即对称轴
在t∈(0,1)上为减函数,即对称轴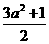 ≥1,∴
≥1,∴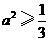 ,∴实数
,∴实数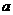 的取值范围是
的取值范围是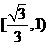 ,选B.
,选B.
★10、(04年湖南文科)若直线y=2a与函数y=|ax-1|(a>0,且a≠1)的图象有两个公共点,则a的取值范围是_______.(0,)
★11、已知f(x)=,求f()+f()+f()+…+f()之值。(答案:500)
★12、已知f(x)= +,求证:f(x)为奇函数。
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十四:对数与对数运算(两课时)
撰稿: 方锦昌 电子邮箱 fangjingchang2007@ 手机号码 13975987411
(四)教学指数函数的应用模型:
①★ 出示例1:我国人口问题非常突出,在耕地面积只占世界7%的国土上,却养育着22%的世界人口.因此,中国的人口问题是公认的社会问题.2000年第五次人口普查,中国人口已达到13亿,年增长率约为1%.为了有效地控制人口过快增长,实行计划生育成为我国一项基本国策.
(Ⅰ)按照上述材料中的1%的增长率,从2000年起,x年后我国的人口将达到2000年的多少倍?
(Ⅱ)从2000年起到2020年我国的人口将达到多少?
★ ② 练习: 2005年某镇工业总产值为100亿,计划今后每年平均增长率为8%, 经过x年后的总产值为原来的多少倍? → 变式:多少年后产值能达到120亿?
(二)、讲授新课:
1.教学指数函数模型思想及指数函数概念:
① 探究两个实例:
●A.细胞分裂时,第一次由1个分裂成2个,第2次由2个分裂成4个,第3次由4个分裂成8个,如此下去,如果第x次分裂得到y个细胞,那么细胞个数y与次数x的函数关系式是什么?
◆B.一种放射性物质不断变化成其他物质,每经过一年的残留量是原来的84%,那么以时间x年为自变量,残留量y的函数关系式是什么?
② 讨论:上面的两个函数有什么共同特征?底数是什么?指数是什么?
③ 定义:一般地,函数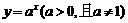 叫做指数函数(exponential function),其中x是自变量,函数的定义域为R.
叫做指数函数(exponential function),其中x是自变量,函数的定义域为R.
④讨论:为什么规定 >0且
>0且 ≠1呢?否则会出现什么情况呢?→ 举例:生活中其它指数模型?
≠1呢?否则会出现什么情况呢?→ 举例:生活中其它指数模型?
2. 教学指数函数的图象和性质:
①、
作图:在同一坐标系中画出下列函数图象: 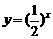 ,
, 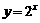 (师生共作→小结作法)
(师生共作→小结作法)
②、 根据图象归纳:指数函数的性质 (书P56)
③、★ 出示P56:例6. 函数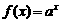 (
(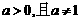 )的图象经过点(3,
)的图象经过点(3, ),求
),求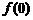 ,
,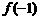 ,
,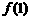 的值.
的值.
④、★出示例7. 比较下列各组中两个值的大小: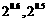 ;
; 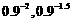 ;
; 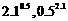 ;
; 
⑤、比较大小: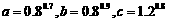 ;
;
(一)、复习提问:
①零指数幂:a0=_____(a≠0);②、负整数指数幂:a-p=_____(
a≠0,p∈N*);④正分数指数幂: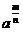 =_____(a>0,m、n∈N*,n>1);⑤负分数指数幂:
=_____(a>0,m、n∈N*,n>1);⑤负分数指数幂: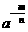 =_____( a>0,m、n∈N*,n>1);
=_____( a>0,m、n∈N*,n>1);
2、 熟练掌握指数函数概念、图象、性质;掌握指数形式的函数定义域、值域,判断其单调性;培养学生数学应用意识
1、 使学生了解指数函数模型的实际背景,认识数学与现实生活及其他学科的联系;理解指数函数的的概念和意义,能画出具体指数函数的图象,掌握指数函数的性质.
(五)、巩固提高练习:
●★[题1](2005年上海高考)方程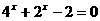 的解是__________
的解是__________
●解答: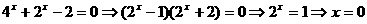
★题2、(2003年上海20题12分)已知函数f(x)=,g(x)=;(1)、证明:函数f(x)为奇函数,并求出f(x)的单调区间;(2)、分别计算f(4)-5 f(2)g(2)和f(9)-5 f(3)g(3),并概括出涉及函数f(x)和g(x)的对所有不为0的实数x都成立的一个等式,并加以证明。
●解:单调↗为(-∞,0)和(0,+∞);(2)、f(4)-5 f(2)g(2)=f(9)-5 f(3)g(3)=0,一般地。有:f(x2)-5 f(x)g(x)=0.
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十三: 指数函数及其性质
撰稿: 方锦昌 电子邮箱 fangjingchang2007@ 手机号码 13975987411
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com