
题目列表(包括答案和解析)
(一)、复习准备:
1、对数概念:若ab=N,⇔则有b=logaN (常用对数lgN,自然对数lnN)Þ负数和零没有对数。
2、对数的运算性质:(换底公式的应用):①loga1=0; ② logaa=1; ③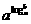 =_____; ④logab·logbc=____; ⑤ logab·logba=____;
⑥
=_____; ④logab·logbc=____; ⑤ logab·logba=____;
⑥ =___; ⑦loga(M·N)=____;
=___; ⑦loga(M·N)=____;
⑧loga()= _______; ⑨logaNb=____
(七)、课堂回顾与总结:
对数及其运算的基本知识体系:
1、对数概念:若ab=N,⇔则有b=logaN (常用对数lgN,自然对数lnN)Þ负数和零没有对数。
2、对数的运算性质:(换底公式的应用):①loga1=0; ② logaa=1; ③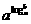 =_____; ④logab·logbc=____; ⑤ logab·logba=____;
⑥
=_____; ④logab·logbc=____; ⑤ logab·logba=____;
⑥ =___; ⑦loga(M·N)=____;
=___; ⑦loga(M·N)=____;
⑧loga()= _______; ⑨logaNb=____
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十五:对数函数及其性质(两课时)
撰稿: 方锦昌 电子邮箱 fangjingchang2 007@ 手机号码 13975987411
课时一:
(六)、学生作业:
◆1、如果在今后若干年内,我国的国民经济生产总值都在平均每年增长9%的水平,则要达到国民经济生产总值比1995年翻两番的年份大约是哪一年?
解:a(1+9%)x=4a,x= =≈16,即经过16年,即要到2011年我国国民经济生产总值比1995年翻两番。(计算时取lg2=0.3;lg109=2.04)
★[题2](200 7年湖南· T1)、若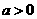 ,
,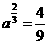 ,则
,则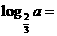 .答案为:3
.答案为:3
★[题3]函数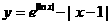 的图象大致是( )
的图象大致是( )

●解: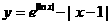 =
=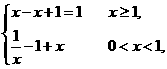 选(D)
选(D)
(五)、课堂巩固练习:
1. 计算: 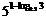 ;
; 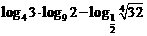

2. 我国的GDP年平均增长率保持为7.3%,约多少年后我国的GDP在1999年的基础上翻两翻?
(四)、实际应用练习:
★ 出示例5:(P66) 20世纪30年代,查尔斯.里克特制订了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大. 这就是我们常说的里氏震级M,其计算公式为: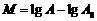 ,其中A是被测地震的最大振幅,
,其中A是被测地震的最大振幅,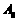 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中距离造成的偏差).
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中距离造成的偏差).
(Ⅰ)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅是20,此时标准地震的振幅是0.001, 计算这次地震的震级(精确到0.1);(Ⅱ)5级地震给人的振感已比较明显,计算7.6级地震最大振幅是5级地震最大振幅的多少倍?(精确到1)
●分析解答:读题摘要 → 数量关系 → 数量计算 → 如何利用对数知识?
③ 出示例6: 当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.根据些规律,人们获得了生物体碳14含量P与生物死亡年数t之间的关系.回答下列问题:(Ⅰ)求生物死亡t年后它机体内的碳14的含量P,并用函数的观点来解释P和t之间的关系,指出是我们所学过的何种函数?(Ⅱ)已知一生物体内碳14的残留量为P,试求该生物死亡的年数t,并用函数的观点来解释P和t之间的关系,指出是我们所学过的何种函数?(Ⅲ)长沙马王墓女尸出土时碳14的余含量约占原始量的76.7%,试推算古墓的年代?
●分析解答:读题摘要 → 寻找数量关系 → 强调数学应用思想
⑤探究训练:讨论展示并分析自己的结果,试分析归纳,能总结概括得出什么结论?
结论:P和t之间的对应关系是一一对应;P关于t的指数函数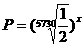 ;
;
思考:t关于P的函数? (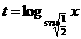 )
)
2. 小结:初步建模思想(审题→设未知数→建立x与y之间的关系→); 用数学结果解释现象
(三)、巩固练习:
1. 设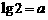 ,
,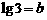 ,试用
,试用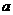 、
、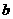 表示
表示 .
.
变式:已知lg2=0.3010,lg3=0.4771,求lg6、lg12、lg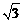 的值.
的值.
2. 计算: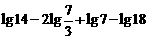 ;
; 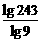 ;
; 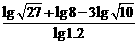 .
.
3. 试求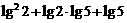 的值
的值
*4. 设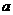 、
、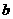 、
、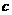 为正数,且
为正数,且 ,求证:
,求证: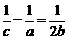
5. 已知
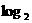 3 = a,
3 = a, 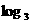 7 = b, 用
a, b 表示
7 = b, 用
a, b 表示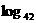 56
56
6. 问题:1995年我国人口总数是12亿,如果人口的年自然增长率控制在1.25℅,问哪一年我国人口总数将超过14亿? (答案: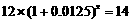 →
→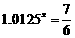 →
→ 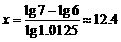 )
)
(二)、讲授新课:
1. 教学对数运算性质及推导:
① 引例: 由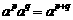 ,如何探讨
,如何探讨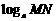 和
和 、
、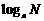
 之间的关系?
之间的关系?
设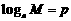 ,
, 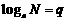 ,由对数的定义可得:M=
,由对数的定义可得:M=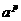 ,N=
,N=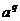
 ∴MN=
∴MN=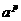
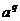 =
=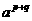
∴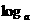 MN=p+q,即得
MN=p+q,即得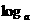 MN=
MN=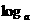 M +
M + 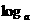 N
N
② 探讨:根据上面的证明,能否得出以下式子?
如果 a > 0,a ¹ 1,M > 0, N > 0 ,则
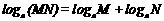 ;
; 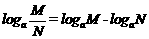 ;
; 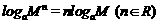
③ 讨论:自然语言如何叙述三条性质? 性质的证明思路?(运用转化思想,先通过假设,将对数式化成指数式,并利用幂运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式 )
)
2.教学例题:
① 出示例1. 用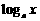 ,
,  ,
, 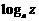 表示下列各式:
表示下列各式: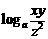 ;
; 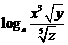
(学生讨论:如何运用对数运算性质? → 师生共练 → 小结:对数运算性质的运用)
② 出示例2. 计算: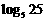 ;
; ;
;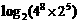 ;lg
;lg
③ 探究:根据对数的定义推导换底公式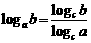 (
(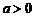 ,且
,且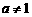 ;
;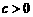 ,且
,且 ;
;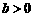 ).
).
作用:化底 → 应用:2000年人口数13亿,年平均增长率1℅,多少年后可以达到18亿?
④ 练习:运用换底公式推导下列结论: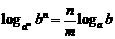 ;
;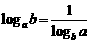
(一)、复习准备:
1.
提问:对数是如何定义的? → 指数式与对数式的互化: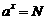

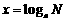
2. 提问:指数幂的运算性质?
3. 作业:书P74:1、2、3、4题
第二课时: 2.2.1对数与对数运算(二)
2.计算: 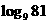 ;
; 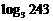 ;
;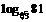 ;
; 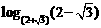 ;
; 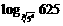 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com