
题目列表(包括答案和解析)
(一)、新课引入:
◆实例分析:见书本P77五个实例:
(七)、课后巩固练习(供选择之用):
★[题1]已知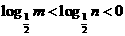 ,则( D )
,则( D )
(A) n<m < 1 (B) m<n< 1 (C) 1< m<n (D) 1 <n<m
★[题2]设f(x)=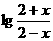 ,则
,则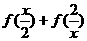 的定义域为(B)
的定义域为(B)
A. 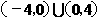 B.(-4,-1)
B.(-4,-1)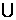 (1,4) C. (-2,-1)
(1,4) C. (-2,-1)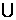 (1,2) D. (-4,-2)
(1,2) D. (-4,-2)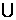 (2,4)
(2,4)
★[题5]方程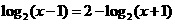 的解为
的解为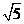 .
.
解: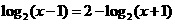 Û
Û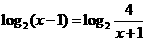 ;即
;即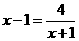 解得
解得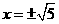 (负值舍去)
(负值舍去)
★[题7] 函数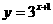
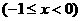 的反函数是( D
)
的反函数是( D
)
A.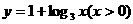 B.
B.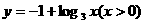
C.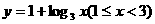 D.
D.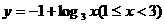
8.已知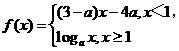 是(-
是(- ,+
,+ )上的增函数,那么a的取值范围是
)上的增函数,那么a的取值范围是
(A)(1,+ ) (B)(-
) (B)(- ,3) (C)[
,3) (C)[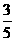 ,3) (D)(1,3)
,3) (D)(1,3)
解:依题意,有a>1且3-a>0,解得1<a<3,又当x<1时,(3-a)x-4a<3-5a,当x³1时,logax³0,所以3-5a£0解得a³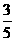 ,所以1<a<3故选D
,所以1<a<3故选D
9.(福建卷)已知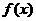 是周期为2的奇函数,当
是周期为2的奇函数,当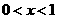 时,
时,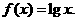 设
设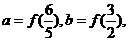
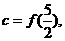 则(A)
则(A)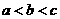 (B)
(B)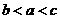 (C)
(C)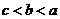 (D)
(D)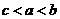
解:已知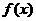 是周期为2的奇函数,当
是周期为2的奇函数,当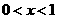 时,
时,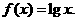 设
设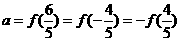 ,
,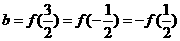 ,
,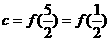 <0,∴
<0,∴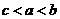 ,选D.
,选D.
11.(辽宁卷)与方程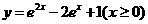 的曲线关于直线
的曲线关于直线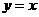 对称的曲线的方程为
对称的曲线的方程为
(A)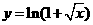 (B)
(B) 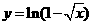 (C)
(C) 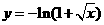 (D)
(D) 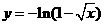
解: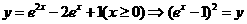 ,
,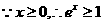 ,即:
,即: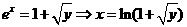 ,所以
,所以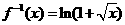 ,故选择答案A。
,故选择答案A。
12.(全国卷I)已知函数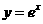 的图象与函数
的图象与函数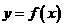 的图象关于直线
的图象关于直线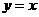 对称,则
对称,则
A、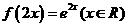 B、
B、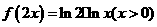 C、
C、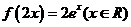 D.
D.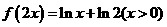
解:函数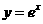 的图象与函数
的图象与函数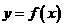 的图象关于直线
的图象关于直线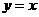 对称,所以
对称,所以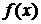 是
是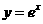 的反函数,即
的反函数,即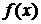 =
= ,∴
,∴ 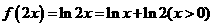 ,选D.
,选D.
13.(全国II)函数y=f(x)的图像与函数g(x)=log2x(x>0)的图像关于原点对称,则f(x)的表达式为
(A) f(x)=(x>0) (B ) f(x)=log2(-x)(x<0) (C) f(x)=-log2x(x>0) (D) f(x)=-log2(-x)(x<0)
解析:(x,y)关于原点的对称点为(-x,-y),所以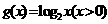
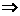
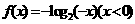 选D
选D
本题主要考察对称的性质和对数的相关性质,比较简单,但是容易把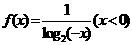 与
与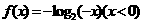 搞混,其实
搞混,其实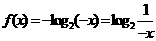
14.(山东卷)设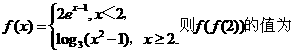 (A)0 (B)1
(C)2
(D)3
(A)0 (B)1
(C)2
(D)3
解:f(f(2))=f(1)=2,选C
15.(陕西卷)设函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b等于( )A.6 B.5 C.4 D.3
解析:函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图象过点(2,8),
则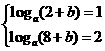 ,∴
,∴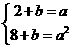 ,
,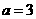 或
或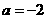 (舍),b=1,∴a+b=4,选C.
(舍),b=1,∴a+b=4,选C.
20.(辽宁卷)设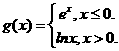 则
则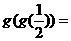 __________[解析]
__________[解析]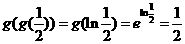 .
.
21.(辽宁卷)方程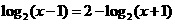 的解为 ________
的解为 ________
解: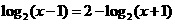 Û
Û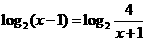 ,即
,即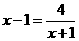 解得
解得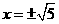 (负值舍去),所以
(负值舍去),所以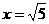 。
。
22.(上海卷)若函数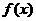 =
=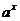 (
(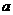 >0,且
>0,且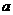 ≠1)的反函数的图像过点(2,-1),则
≠1)的反函数的图像过点(2,-1),则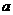 = .
= .
解:由互为反函数关系知,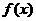 过点
过点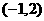 ,代入得:
,代入得: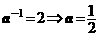 ;
;
23.(上海卷)方程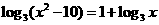 的解是_______.
的解是_______.
解:方程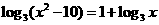 的解满足
的解满足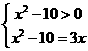 ,解得x=5.
,解得x=5.
25.(重庆卷)设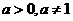 ,函数
,函数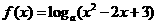 有最小值,则不等式
有最小值,则不等式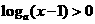 的解集为
。
的解集为
。
解:由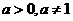 ,函数
,函数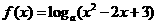 有最小值可知a>1,所以不等式
有最小值可知a>1,所以不等式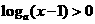 可化为x-1>1,即x>2.
可化为x-1>1,即x>2.
26.(上海春)方程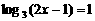 的解
的解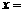 .
.
解:由log3(2x-1),化为同底数的对数,得log3(2x-1)=log33,2x-1=3 ,即 x=2 .从而应填2.
27、(04年湖南文科)若直线y=2a与函数y=|ax-1|(a>0,且a≠1)的图象有两个公共点,则a的取值范围是_______.(0,1/2)
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十六: 幂函数
撰稿: 方锦昌 电子邮箱 fangjingchang2 007@ 手机号码 13975987411
(七)相关高考题摘录(供课时选择之用):
★[例题1]函数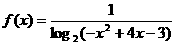 的定义域为( A
)
的定义域为( A
)
A.(1,2)∪(2,3)B. C.(1,3)D.[1,3]
C.(1,3)D.[1,3]
[★题3]函数¦(x)=的定义域为____({x|1<x≤2})
[★题4]函数y= 的单调递增区间为___([2,6)注意6是达不到的)
[★题5]函数y=lg(mx2-4mx+m+3);①当定义域为R时,求m的取值范围; ②当值域为R时,求m的取值范围。 解、①{m|0≤m<1} ②{m|m≥1 或m<0}
[★题8]解不等式log2(-x)<x+3的解集为( D )
A (-∞,-1) B (-∞,-2) C (-1,0) D (-2,0)
★[例题9]设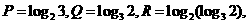 则( )
则( )
(A)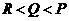 (B)
(B)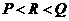 (C)
(C)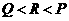 (D)
(D)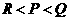
 解:
解: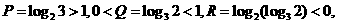 则
则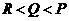 ,选A.
,选A.
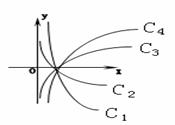
※ [★题11]如图中的曲线是对数函数y=logax 的图象,已知a取, , ,四个值,则相应于曲线c1,c2,c3,c4 的a之值依次为_________
※
[★题12]设a>0,a≠1,函数¦(x)=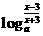 ,g(x)=1+loga(x-1)
,g(x)=1+loga(x-1)
① 求 ¦(x) 和 g(x)的定义域的公共部分D,并判定¦(x)在D内的单调性;若[m,n]ÜD,且¦(x)在[m,n]上的值域恰好为[g(n), g(m)],求a的取值范围
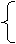 解、① >0
解、① >0
x-1>0 Þx>3 则D={x|x>3};②当0<a<1时, ¦(x)为↘;当a>1时, ¦(x)为↗
③由g(n)< g(m)则loga(n-1)< loga(m-1) 而m<n,则0<a<1,故¦(x)为↘
则¦(n)= g(n), ¦(m)= g(m)其中3<m<n,故方程¦(x)= g(x)有两个大于3的不同实根,⇔ 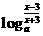 =1+loga(x-1)有大于3的两个实根⇔方程ax2+(2a-1)x+3(1-a)=0有两个大于3的实根⇔
=1+loga(x-1)有大于3的两个实根⇔方程ax2+(2a-1)x+3(1-a)=0有两个大于3的实根⇔
△
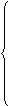 >0
>0
>3
0<a<1
a·32+(2a-1)·3+3(1-a)>0 ∴0<a<为所求
(六)、课后提高作业
1.求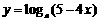 的单调递增区间;
的单调递增区间;
2.已知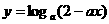 在[0,1]上是
在[0,1]上是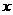 的减函数,求
的减函数,求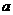 的取值范围
的取值范围
(五)、巩固补充练习
1.比较大小: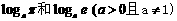 ;
;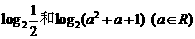
2.已知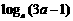 恒为正数,求
恒为正数,求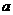 的取值范围.
的取值范围.
3.求函数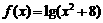 的定义域及值域.
的定义域及值域.
4.函数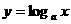 在[2,4]上的最大值比最小值大1,求
在[2,4]上的最大值比最小值大1,求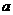 的值;
的值;
5. 求函数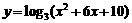 的最小值.
的最小值.
6. 求下列函数的反函数:
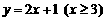 ;
; 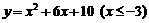 ;
; 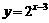 ;
; 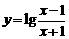
(四)、提高练习:
★1题.(1)证明函数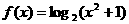 在
在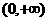 上是增函数(可利用复合函数法去处理)。(2)、探究:函数
上是增函数(可利用复合函数法去处理)。(2)、探究:函数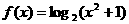 在
在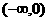 上是减函数还是增函数?(可利用偶函数的性质去处理)。
上是减函数还是增函数?(可利用偶函数的性质去处理)。
2. 求函数 的单调区间.(强调:复合函数的单调性:同增异减,注意利用图象处理)
的单调区间.(强调:复合函数的单调性:同增异减,注意利用图象处理)
(三)、巩固练习:
1.求下列函数的反函数: y=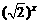 (x∈R); y=
(x∈R); y=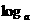
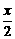 (a>0,a≠1,x>0)
(a>0,a≠1,x>0)
2.己知函数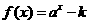 的图象过点(1,3)其反函数
的图象过点(1,3)其反函数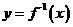 的图象过(2,0)点,求
的图象过(2,0)点,求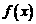 的表达式.
的表达式.
(二)、讲授新课:
1. 教学对数函数模型思想及应用:
出示P72:例题9:溶液酸碱度的测量问题:溶液酸碱度pH的计算公式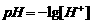 ,其中
,其中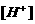 表示溶液中氢离子的浓度,单位是摩尔/升. (Ⅰ)分析溶液酸碱读与溶液中氢离子浓度之间的关系?
(Ⅱ)纯净水
表示溶液中氢离子的浓度,单位是摩尔/升. (Ⅰ)分析溶液酸碱读与溶液中氢离子浓度之间的关系?
(Ⅱ)纯净水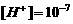 摩尔/升,计算纯净水的酸碱度.
摩尔/升,计算纯净水的酸碱度.
2.反函数的教学:
①、
分析:函数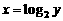 由
由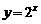 解出,是把指数函数
解出,是把指数函数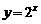 中的自变量与因变量对调位置而得出的. 习惯上我们通常用x表示自变量,y表示函数,即写为
中的自变量与因变量对调位置而得出的. 习惯上我们通常用x表示自变量,y表示函数,即写为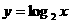 .那么我们就说指数函数
.那么我们就说指数函数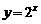 与对数函数
与对数函数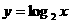 互为反函数
互为反函数
②、在同一平面直角坐标系中,画出指数函数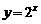 及其反函数
及其反函数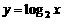 图象,发现什么性质?
图象,发现什么性质?
③、
探究:如果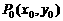 在函数
在函数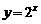 的图象上,那么P0关于直线
的图象上,那么P0关于直线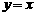 的对称点在函数
的对称点在函数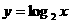 图象上吗,为什么?由上述过程可以得到什么结论?(互为反函数的两个函数的图象关于直线
图象上吗,为什么?由上述过程可以得到什么结论?(互为反函数的两个函数的图象关于直线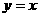 对称)
对称)
(一)、复习准备:
提问:对数函数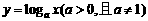 的图象和性质?
的图象和性质?
(二)、讲授新课:
1.教学对数函数的图象和性质:
①
定义:一般地,当a>0且a≠1时,函数 叫做对数函数(logarithmic function).
叫做对数函数(logarithmic function).
自变量是x; 函数的定义域是(0,+∞)
②
辨析: 对数函数定义与指数函数类似,都是形式定义,注意辨别,如: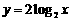 ,
, 都不是对数函数,而只能称其为对数型函数;对数函数对底数的限制
都不是对数函数,而只能称其为对数型函数;对数函数对底数的限制 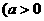 ,且
,且 .
.
③ 探究:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗?
|
名称 |
指数函数 |
对数函数 |
|
一般解析式 |
y=ax (a>0,a≠1) |
y=logax (a>0,a≠1) |
|
定义域 |
|
|
|
值域 |
|
|
|
当a>1时的图像 |
①注意特殊点、单调性、变化范围等。 |
②同一坐标系中两个图像时底数的确定方法。 |
|
当0<a<1时的图像 |
||
|
两者的关系 |
|
2. 教学例题
① 出示P71:例7.求下列函数的定义域: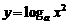 ;
; 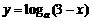 ;
; 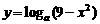
② 出示P72:例8. 比较大小: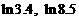 ;
;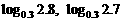 ;
;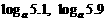
课堂练习:P73:题1、2、3;P74:练习题:7、8、9
课时二|:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com