
题目列表(包括答案和解析)
★1.(北京卷)已知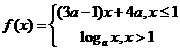 是
是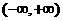 上的减函数,那么
上的减函数,那么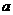 的取值范围是
的取值范围是
(A)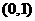 (B)
(B)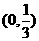 (C)
(C)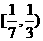 (D)
(D)
●解:依题意,有0<a<1且3a-1<0,解得0<a<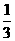 ,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³
,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³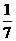 故选C
故选C
★2.(福建卷)已知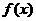 是周期为2的奇函数,当
是周期为2的奇函数,当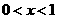 时,
时,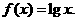 设
设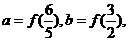
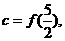 则
则
(A)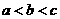 (B)
(B)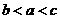 (C)
(C)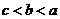 (D)
(D)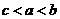
●解:已知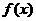 是周期为2的奇函数,当
是周期为2的奇函数,当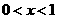 时,
时,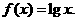 设
设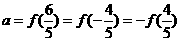 ,
,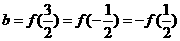 ,
,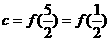 <0,∴
<0,∴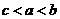 ,选D.
,选D.
★3.(湖南卷)函数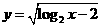 的定义域是( )
的定义域是( )
A.(3,+∞) B.[3, +∞) C.(4, +∞) D.[4, +∞)
●解:函数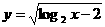 的定义域是
的定义域是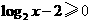 ,解得x≥4,选D.
,解得x≥4,选D.
★4.(陕西卷)设函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b等于( )
A.6 B.5 C.4 D.3
●解析:函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图象过点(2,8),
则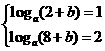 ,∴
,∴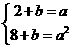 ,
,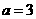 或
或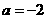 (舍),b=1,∴a+b=4,选C.
(舍),b=1,∴a+b=4,选C.
★5.(重庆卷)已知定义域为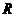 的函数
的函数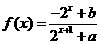 是奇函数。(Ⅰ)求
是奇函数。(Ⅰ)求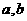 的值;(Ⅱ)若对任意的
的值;(Ⅱ)若对任意的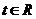 ,不等式
,不等式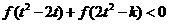 恒成立,求
恒成立,求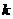 的取值范围;
的取值范围;
●解析:(Ⅰ)因为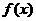 是奇函数,所以
是奇函数,所以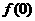 =0,即
=0,即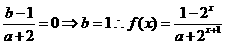
又由f(1)= -f(-1)知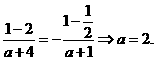
(Ⅱ)解法一:由(Ⅰ)知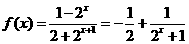 ,易知
,易知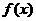 在
在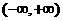 上
上
为减函数。又因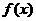 是奇函数,从而不等式:
是奇函数,从而不等式: 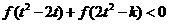
等价于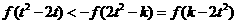 ,因
,因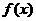 为减函数,由上式推得:
为减函数,由上式推得:
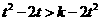 .即对一切
.即对一切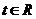 有:
有: ,从而判别式
,从而判别式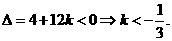
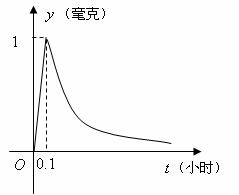 ★6、(07湖北)为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
★6、(07湖北)为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为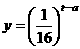 (a为常数),如图所示,根据图中提供的信息,回答下列问题:
(a为常数),如图所示,根据图中提供的信息,回答下列问题:
(Ⅰ)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为 .
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过 小时后,学生才能回到教室.
解: 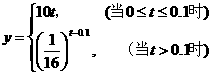 ;
; 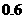
★7、(07安徽)若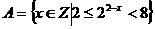
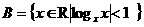 ,
,
则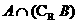 的元素个数为A.0 B.1 C.2 D.3 (C)
的元素个数为A.0 B.1 C.2 D.3 (C)
(07安徽)设a>1,且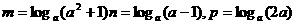 ,则
,则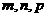 的大小关系为( B )
的大小关系为( B )
(A) n>m>p (B) m>p>n (C) m>n>p (D) p>m>n
★8、(07重庆)若函数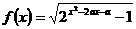 的定义域为R,则实数
的定义域为R,则实数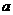 的取值范围 。
的取值范围 。
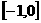
5. 计算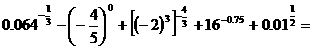 .
.
★[题6]. 求下列函数的值域:
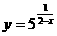 ;
; 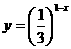 ;
; 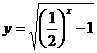 ;
; 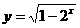
●★[题7]设函数¦(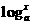 )= (x-x-1) 其中a>0且a≠1
)= (x-x-1) 其中a>0且a≠1
① 求¦(x)及其单调性和奇偶性;②当x∈(-1,1)时,¦(1-m)+¦(1-m2)<0恒成立,求m的取值范围;③当x∈(-∞,2)时, ¦(x)- 4的值恒为负数,求a的取值范围
◆ 解、①、¦(x)=(ax-a-x);
②、由复合函数法有:¦(x)为↗,由定义知¦(x)为奇函数; ③{m|1<m<}④ 即考查¦(2)- 4 ≤0则{a|2-≤a≤2+且a ≠1}
4. 函数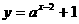 (
(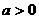 ,且
,且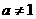 )的图象必经过点 .
)的图象必经过点 .
3. 若点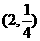 既在函数
既在函数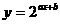 的图象上,又在它的反函数的图象上,则
的图象上,又在它的反函数的图象上,则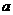 =______,
=______,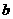 =_______
=_______
2. 函数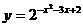 的单调区间为__________________.
的单调区间为__________________.
1.函数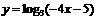 的定义域为________,值域为__________.
的定义域为________,值域为__________.
例1、函数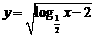 的定义域为_____________________.
的定义域为_____________________.
例2、函数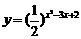 的单调区间为_____________________.
的单调区间为_____________________.
例3、已知函数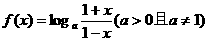 .判断
.判断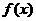 的奇偶性并予以证明.
的奇偶性并予以证明.
例4、按复利计算利息的一种储蓄,本金为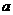 元,每期利率为
元,每期利率为 ,设本利和为
,设本利和为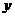 元,存期为
元,存期为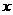 ,写出本利和
,写出本利和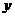 随存期
随存期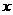 变化的函数解析式. 如果存入本金1000元,每期利率为2.25%,试计算5期后的本利和是多少(精确到1元)?(复利是一种计算利息的方法,即把前一期的利息和本金加在一起算做本金,再计算下一期的利息. )
变化的函数解析式. 如果存入本金1000元,每期利率为2.25%,试计算5期后的本利和是多少(精确到1元)?(复利是一种计算利息的方法,即把前一期的利息和本金加在一起算做本金,再计算下一期的利息. )
▲小结与要求:掌握指数函数、对数函数、幂函数的图象与性质,会用函数性质解决一些简单的应用问题. )
(一)、复习归纳:
1. 提问:指数函数、对数函数、幂函数的图象和性质(比较一次函数、二次函数、反比例函数)
|
|
指数函数y=ax(a>0,a≠1) |
对数函数y=logax(a>0,a≠1) |
幂函数y=xa |
|
函数图象 |
|
|
|
|
定义域 |
|
|
|
|
值域 |
|
|
|
|
单调性 |
|
|
|
|
奇偶性 |
|
|
|
|
特殊点、线 |
|
|
|
2. 求下列函数的定义域: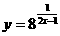 ;
;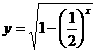 ;
;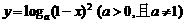
3. 比较下列各组中两个值的大小: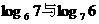 ;
;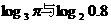 ;
;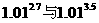
(三)、练习及其应用
1、学法大视野:P26:求幂函数的解析式的基本方法:
例:幂函数y=f(x)的图象过点(3,),求出其解析式。(y= y=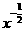 )
)
2. 讨论函数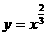 的定义域、奇偶性,作出它的图象,并根据图象说明函数的单调性.
的定义域、奇偶性,作出它的图象,并根据图象说明函数的单调性.
3.利用幂函数的图象的特征解题:±2、±
4、利用幂函数的单调性比较幂的大小: 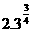 与
与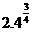 ;
;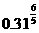 与
与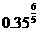 ;
;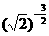 与
与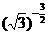 .
.
5、用数形结合的思想,求参数的取值范围: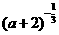 <
< 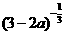 求a的取值范围。(a∈(-∞,-2)∪(,)
求a的取值范围。(a∈(-∞,-2)∪(,)
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义十七:基本初等函数的归纳与概括应用
撰稿: 方锦昌 电子邮箱 fangjingchang2 007@ 手机号码 13975987411
(二)、讲授新课:
1、教学幂函数的图象与性质
■① 给出定义:一般地,形如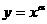
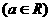 的函数称为幂函数,其中
的函数称为幂函数,其中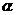 为常数.
为常数.
■②练:在函数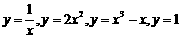 中,哪几个函数是幂函数?(书本P79:习题第1题)
中,哪几个函数是幂函数?(书本P79:习题第1题)
■③ 作出下列函数的图象:(1)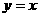 ;(2)
;(2)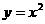 ;(3)
;(3)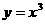 ;(4)
;(4)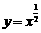 ;(5).
;(5).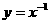
▲ ④
引导学生观察图象,归纳概括幂函数的的性质及图象变化规律:
④
引导学生观察图象,归纳概括幂函数的的性质及图象变化规律:
(Ⅰ)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1);
(Ⅱ)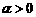 时,幂函数的图象通过原点,并且在区间
时,幂函数的图象通过原点,并且在区间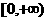 上是增函数.特别地,当
上是增函数.特别地,当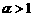 时,幂函数的图象下凸(称为凸函数);当
时,幂函数的图象下凸(称为凸函数);当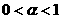 时,幂函数的图象上凸(称为凹函数);
时,幂函数的图象上凸(称为凹函数);
(Ⅲ)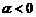 时,幂函数的图象在区间
时,幂函数的图象在区间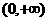 上是减函数.在第一象限内,当
上是减函数.在第一象限内,当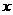 从右边趋向原点时,图象在
从右边趋向原点时,图象在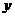 轴右方无限地逼近
轴右方无限地逼近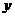 轴正半轴,当
轴正半轴,当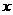 趋于
趋于 时,图象在
时,图象在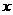 轴上方无限地逼近
轴上方无限地逼近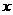 轴正半轴.
轴正半轴.
2、教学例题:
 ★出示P78:书本之例1:讨论
★出示P78:书本之例1:讨论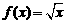 在
在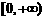 的单调性.
的单调性.
◆3、小结:幂函数y=xa=xq/p的的性质及图象变化规律可以分为以下几类:
★1、直线类:y=x0,y=x
★2、抛物线类:y=x2,y=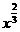 ,y=
,y=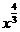 ……(即q是偶数,p是奇数,a=大于零)
……(即q是偶数,p是奇数,a=大于零)
性质有;(1)、必过点(0,0)、(1,1)、(-1,1);(2)定义域为R,且在(0,+∞)上为增函数,为偶函数;
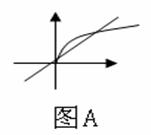
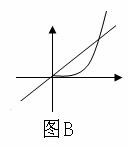
(3)在第一象限内:当0<a<1时:为图(A)所示形式(上凸,称为凹函数);当a>1时:如图B所示(下凸,称为凸函数)
★3、拐线类:y=x3,y= y=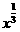 ,y= y=
,y= y=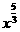 ,y y=
,y y=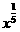 ……(即q是奇数,p是奇数,a=大于零);性质有;(1)、必过点(0,0)、(1,1)、(-1,-1);
……(即q是奇数,p是奇数,a=大于零);性质有;(1)、必过点(0,0)、(1,1)、(-1,-1);
(2)定义域为R,在(0,+∞)上为增函数,为奇函数;(3)在第一象限内:当0<a<1时:为图(A)所示形式(上凸,称为凹函数);当a>1时:如图B所示(下凸,称为凸函数)
★4、双曲线类:y=x-1,y=x-3,……(即p为奇数,且a=q/p<0时) ……性质有;(1)、必过点(1,1);(2)定义域为{x|x≠0},在(0,+∞)上为减函数;
★5、半支抛物线类:y= y=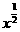 ;y= y=
;y= y= …(即p为偶数,且a=q/p>0时)图象过点(0,0)、(1,1);定义域为{x|x>0};图象只位于第一象限之内,且为增函数;
…(即p为偶数,且a=q/p>0时)图象过点(0,0)、(1,1);定义域为{x|x>0};图象只位于第一象限之内,且为增函数;
而y= y=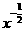 , y=
, y=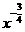 …(即p为偶数,且a= <0时): 图象过点(1,1)定义域为{x|x>0};图象只位于第一象限之内,且为减函数。
…(即p为偶数,且a= <0时): 图象过点(1,1)定义域为{x|x>0};图象只位于第一象限之内,且为减函数。
总之:当a>0时,幂函数y=xa为增函数,当a<0时,幂函数y=xa为减函数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com