
题目列表(包括答案和解析)
7.若不等式ax2+bx+2>0的解集是{x| -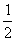 < x <
< x < },则a + b的值为
},则a + b的值为
(A) -10 (B) -14 (C) 10 (D) 14
6、 设x,y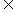 R+,且xy-(x+y)=1,则
R+,且xy-(x+y)=1,则
(A)
x+y 2
2 +2 (B) xy
+2 (B) xy
 +1
(C) x+y
+1
(C) x+y (
( +1)2 (D)xy
+1)2 (D)xy 2
2 +2
+2
5、若a,b,c成等比数列,m是a,b的等差中项,n是b,c的等差中项,则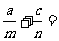
(A)4 (B)3 (C)2 (D)1
4、下列结论正确的是
(A)当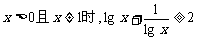 (B)
(B)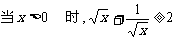
(C)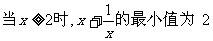 (D)
(D)
3、已知数列{an}是公比q≠1的等比数列,则在 “(1){anan+1}, (2){an+1-an}, (3){an3},(4){nan}”这四个数列中,成等比数列的个数是
(A)1 (B)2 (C)3 (D)4
2、对于任意实数a、b、c、d,命题①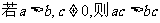 ;②
;②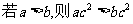 ③
③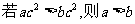 ;④
;④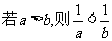 ;⑤
;⑤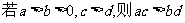 .其中真命题的个数是
.其中真命题的个数是
(A)1 (B)2 (C)3 (D)4
1、下列命题中正确的是
(A)若a,b,c是等差数列,则log2a,log2b,log2c是等比数列
(B)若a,b,c是等比数列,则log2a,log2b,log2c是等差数列
(C)若a,b,c是等差数列,则2a,2b,2c是等比数列
(D)若a,b,c是等比数列,则2a,2b,2c是等差数列
(Ⅰ)求数列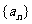 的通项公式;
的通项公式;
(Ⅱ)证明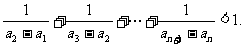
(I)解:设等差数列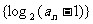 的公差为d.
的公差为d.
由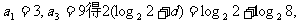 即d=1.
即d=1.
所以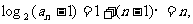 即
即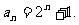
(II)证明因为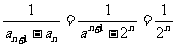 ,
,
所以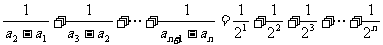
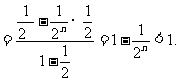
题25. 设{an}是公差d≠0的等差数列,Sn是其前n项的和.
(1)若a1=4,且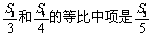 ,求数列{an}的通项公式;
,求数列{an}的通项公式;
(2)是否存在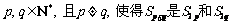 的等差中项?证明你的结论.
的等差中项?证明你的结论.
(1)由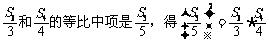 ,
,
即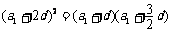 ,
,
将a1=4代入上式并整理得d(12+5d)=0,
因为d≠0,解得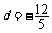 .
.
所以数列{an}的通项公式为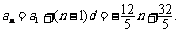
(2)不存在p,q∈N*,且p≠q,使得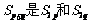 的等差中项.
的等差中项.
证明:因为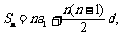 所以
所以
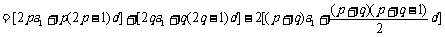
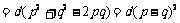 .
.
因为d≠0,且p≠q,
所以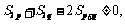
即不存在p,q∈N*,且p≠q,使得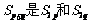 的等差中项.
的等差中项.
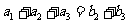 ,
,
(I)
求数列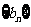 的通项公式;
的通项公式;
(II)
求数列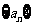 的通项公式.
的通项公式.
解(I)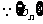 是等比数列,且
是等比数列,且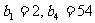 ,
,

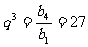 ……………………………………3分
……………………………………3分

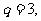
 ……………………6分
……………………6分
(II) 数列
数列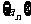 是等差数列,
是等差数列,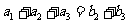 ,
,
又
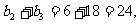
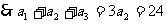
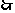
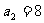 ……………………………………10分
……………………………………10分
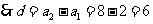
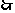
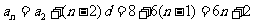 ………………12分
………………12分
题23.已知数列{an}的各项均为正数,Sn为其前n项和,对于任意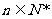 ,满足关系
,满足关系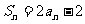 .
.
(Ⅰ)证明:{an}是等比数列;
(Ⅱ)在正数数列{cn}中,设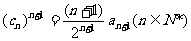 ,求数列{lncn}中的最大项.
,求数列{lncn}中的最大项.
(Ⅰ)证明:∵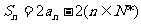 ①
①
∴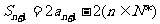 ② …………2分
② …………2分
②-①,得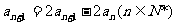
∵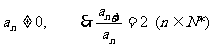
故数列{an}是等比数列 ………………5分
(Ⅱ)解:据(Ⅰ)可知 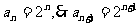
由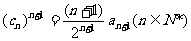 ,得
,得
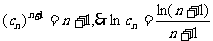 …………8分
…………8分
令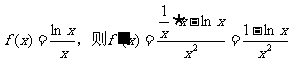
∵在区间(0,e)上,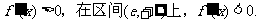
∴在区间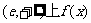 为单调递减函数.
为单调递减函数.
∴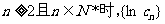 是递减数列 又
是递减数列 又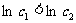
∴数列 中的最大项为
中的最大项为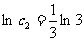 …………12分
…………12分
解∵10Sn=an2+5an+6, ① ∴10a1=a12+5a1+6.
解之,得a1=2,或a1=3.……………………………………………………………2分
又10Sn-1=an-12+5an-1+6(n≥2), ②
由①-②,得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)=0.
∵an+an-1>0,∴an-an-1=5(n≥2).…………………………………………………5分
当a1=3时,a3=13,a15=73.a1, a3,a15不成等比数列,∴a1≠3.
当a1=2时,a3=12,a15=72,有 a32=a1a15.…………………………………………7分
∴数列{bn}是以6为公比,2为首项的等比数列,bn=2×6n-1. ………………………9分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com