
题目列表(包括答案和解析)
12.解:(1)如图,在线段EF上任取一点Q,分别向BC,CD作垂线.
 由题意,直线EF的方程为:+=1
由题意,直线EF的方程为:+=1
(2)设Q(x,20-x),则长方形的面积
S=(100-x)[80-(20-x)] (0≤x≤30)
化简,得 S= -x2+x+6000 (0≤x≤30)
配方,易得x=5,y=时,S最大,其最大值为6017m2
C组:
11.解:(1)可判断A、B在直线l的同侧,设A点关于l的对称点A1的坐标为(x1,y1).
|
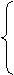
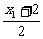 +2·
+2·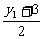 -2=0,
-2=0,
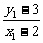 ·(-
·(-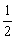 )=-1.
)=-1.
|
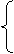 x1=-
x1=-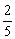 ,
,
y1=-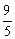 .
.
由两点式求得直线A1B的方程为y=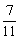 (x-4)+1,直线A1B与l的交点可求得为P(
(x-4)+1,直线A1B与l的交点可求得为P(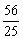 ,-
,-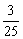 ).由平面几何知识可知|PA|+|PB|最小.
).由平面几何知识可知|PA|+|PB|最小.
(2)由两点式求得直线AB的方程为y-1=-(x-4),即x+y-5=0.
直线AB与l的交点可求得为P(8,-3),它使|PA|-|PB|最大.
10.y=0或3x-4y-3=0.
8. 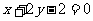 9.
9. 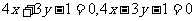 ;
;
6. 4x-3y=0或x+y+7=0
7. 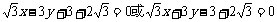
12. 解:当l与线段AB有公共点时,其倾斜角最小为直线PB的倾斜角α,
最大为直线PA的倾斜角为β,
∵直线AP的斜率为KAP=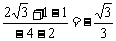 ∴α=1500
∴α=1500
∵直线BP的斜率为KBP=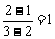 ∴β=450
∴β=450
∴直线l的倾斜角θ的取值范围为:450≤θ≤1500
B组:
11.解:由题意可知:当m≠0时
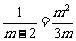 ≠
≠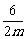 , m-2≠0 ,;解得:m=3,m=-1,m≠±3,m≠2
, m-2≠0 ,;解得:m=3,m=-1,m≠±3,m≠2
当m=0时两直线分别为x+6=0, -2x=0 即 x=-6, x=0 两直线没有公共点
综合以上知:当m=-1,或m=0时两直线没有公共点.
∴m的取值为-1
10.解:先求两直线的交点,联立方程组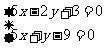 得,
得, .
.
∵ 直线l与直线2x+3y+5=0平行,
∴ 可设直线l的方程为:2x+3y+b=0, 将x=1,y=4代入得b=-14,
故所求直线l的方程为:2x+3y-14=0.
6. 3x – y +2 = 0 7. 9 8.. m≠ 0且m≠ -3 9. x+4y-7=0或x=-1
4、设实数x、y满足不等式组
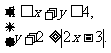
(1)求点(x,y)所在的平面区域;
(2)设 ,在(1)所求的区域内,求函数
,在(1)所求的区域内,求函数 的最值
的最值
答案与提示
A组:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com