22、已知函数f(x)=ax²+(2a-1)x-3 (a≠0)在区间[-3/2，2]上的最大值为1，求实数a的值。(14分)

解：二次函数f(x) =ax²+(2a-1)x-3 (a≠0)的对称轴为

　　 ①若x=-3/2时函数取最大值，则

　　　　　　　　　　　 解得：a=-10/3

　　 此时函数的对称轴为x=-23/20，所以在区间[-3/2，2]上当x=-23/20时函数取最大值。所以a=-10/3不符合题意。

　　 ②若x=2时函数取最大值，则a×2²+(2a-1)×2-3=1,　　 解得：a=3/4

　　 此时函数的对称轴为x=-1/3，所以在区间[-3/2，2]上当x=2时函数取最大值。

　　　　　　　 所以a=3/4符合题意。

　　 ③若时函数取最大值，则

　　　　　　　　　　　　　　　　 解得：

(没打完)

21、已知函数在区间上为增函数，求a的取值范围。(12分)

解：令g(x)=x²-ax-a

　　 ∵f(x)=log_ag(x)在上为增函数，∴g(x)应在上为减函数

　　　 且g(x)>0在上恒成立

因此：　　　 即

　　　 解得：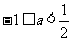

故实数a的取值范围是：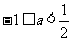

20、某旅游公司有客房300间，每间房租为200元，每天客满，公司欲提高档次，并提高租金。如果每间客房每日增加20元，客房出租就减少10间，若不考虑其他因素，公司将房租提高到多少时，每天客房的租金总收入最高？(10分)

解：设公司将房租提高x个20元，则每天客房的租金收入y为：

y=(200+20x)(300-10x)　　 (x∈N)

　=60000+4000x-200x²

　　　　 这个二次函数图像的对称轴为：

　　　　 200+20x=200+20×10=400

　　 　　当x=10时，y_最大值=80000.

　　 答：将房租提高到400元/间时，客房的租金总收入最高，每天为80000元。

19、已知函数(a为常数)

(1) 证明：函数f(x)在(-∞,+∞)上是减函数；

(2) 若f(x)为奇函数，求a的值。(12分)

(1)证明：在(-∞,+∞)上任取两个点x₁，x₂且x₁＜x₂

　　　　　 f(x₁)-f(x₂)= ()-()

　　　　　　　　　 =-

　　　　　　　　　 =

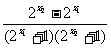
　　　　　　　　　 ∵2>1且x₁＜x₂　 ∴>0而

　　　　　　　　　 ∴f(x₁)-f(x₂)>0即f(x₁)>f(x₂)　 ∴函数f(x)在(-∞,+∞)上是减函数。

　　　　 (2)∵f(x)为奇函数且在x=0处有意义，∴f(0)=0

　　　　　　 ∴　　　　 ∴

18、设函数f(x)=|x²-2x-3|

　　 (1)求函数f(x)的零点；

　 (2)画出函数图像，并写出单调区间。

　解：(1)f(x)=|x²-2x-3|=0，x=3或x=-1　 ∴函数f(x)的零点为x=3或x=-1；

(2)对称轴：x=1　　 单增区间：[-1，1]，

　　　　　　　　　　 单减区间：，[1，3]

17、已知全集U={1，2，3，4，5，6，7，8}，A={x|1≤x≤5，x∈Z}，B={x|2<x<9,x∈Z}。

(1) 求A∩B;

(2) 求(C_UA)∪(C_UB)。(10分)

　　　　 解：(1)A∩B={3，4，5}

　　　　　　 (2)(C_UA)∪(C_UB)= C_U(A∩B)={1，2，6，7，8}

16、给出下列函数：

①　　 函数y=a^x与函数y=log_aa^x(a>0且a≠1)的定义域相同。

②　　 y=x³与y=3^x的值域相同。

③　　 函数与均是奇函数。

④　　 函数y=(x-1)²与y=2x-1在R₊上都是增函数。

　　　 　其中正确命题的序号是__①③__。

15、如果二次函数f(x)=x²-(a-1)x+5在区间上是增函数，那么a的取值范围是

_a≤2__.

14、已知f(x)的定义域为，则函数f(x²)的定义域为______　　 __________。

13、已知映射f：N→N^* ，x→x²+1，则f(x)=0的原象是_____3______。