
题目列表(包括答案和解析)
2、已知实数a, b满足等式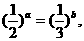 下列五个关系式:①、0<b<a
②、a<b<0
③、0<a<b ④、b<a<0 ⑤、a=b;其中不可能成立的关系式有( )
下列五个关系式:①、0<b<a
②、a<b<0
③、0<a<b ④、b<a<0 ⑤、a=b;其中不可能成立的关系式有( )
A.1个 B.2个 C.3个 D、4个
1、函数y=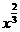 的大致图象是
的大致图象是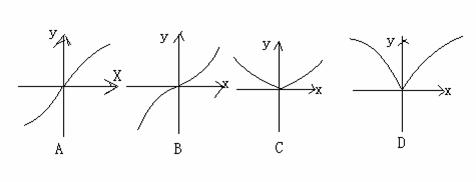
★16题(12分)、①、已知f(x)=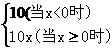 求f[f(-7)]之值。
求f[f(-7)]之值。
(2)、已知f(x)=3x2+1,g(x)=2x-1,求f[g(x)].
★ 17题(12分)、给定集合A、B,定义一种新运算: A*B={ x | x∈A或x∈B,
但xÏA∩B },又已知A={0,1,2,},B={1,2,3},用列举法写出A*B.
★18题(12分)、已知集合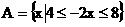 ,集合
,集合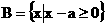 。
。
(1)、若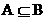 ,求a的范围;
,求a的范围;
(2)、若全集U=R且 ,求a的范围。
,求a的范围。
★19题(13分)、对于函数f(x)=x2-2|x|,
(1)、判断其奇偶性,并指出图象的对称性;
(2)、画此函数的图象,并指出其单调区间。
★20题(13分):有一个小型自来水厂,蓄水池中有水450吨,水厂每小时可向蓄水池注水80吨,同时蓄水池又向居民小区供水,x小时内供水总量为80吨。现在开始向池中注水并同时向居民小区供水,问:
(1)、多少小时后蓄水池中的水量最少?
(2)、如果蓄水池中存水量少于150吨时,就会出现供水紧张,那么有几小时供水紧张?
★21题(13分):已知奇函数f(x)的定义域为(-∞,0)∪(0,+∞),且f(x)在(0,+∞)上为增函数,又f(1)=0,函数g(x)= -x2+mx+1-2m,x∈[0,1]
①、证明函数f(x)在(-∞,0)上也为增函数;
②、解关于x的不等式f(x)<0;
③、当x∈[0,1]时,求使得g(x)<0且f[g(x)]<0恒成立的m的取值范围。
★11、集合{0,1}的所有真子集是_____________________________.
★12、设函数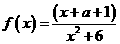 为奇函数,则实数
为奇函数,则实数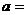 ______________。
______________。
★13、已知函数y=x2-2ax-3在(2,+∞)上是增函数,则a的取值范围是___________.
 ★14、已知集合
★14、已知集合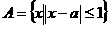 ,
,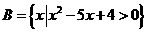 ,若A∩B=Æ,则实数
,若A∩B=Æ,则实数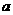 的取值范围是:_____________________________________.
的取值范围是:_____________________________________.
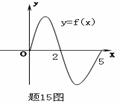
★15、设奇函数f(x)的定义域为[−5,5].若当x∈[0,5]时,f(x)的图象 如右图,则不等式f(x)<0的解集是 .
★1、己知全集I={1,2,3,4,5}, M ={1,2}, N={1,3,5},则M∩CIN等于:
A、{1,2} B、{2,3} C、{2} D、{2,4}
★2、下列函数中既不是奇函数又不是偶函数的是:
A、f(x)=|1-x| B、f(x)=x-x3 C、f(x)=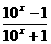 D、f(x)=|x|
D、f(x)=|x|
★3、函数y=ax-1+2(a>0,a≠1)一定经过的定点是:
A、(0,1) B、(1,1) C、 (1,2) D、 (1,3)
★4、函数f(x)=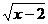 +(x-4)0的定义域为:
+(x-4)0的定义域为:
A. {x|x>2,x≠4} B、{x|x≥2,或x≠4} C、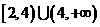 D、
D、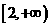
 ★5、函数y=x2-1的值域是:
★5、函数y=x2-1的值域是:
A. (-∞,-1) B、  C、 [-1,0]
D、 R
C、 [-1,0]
D、 R
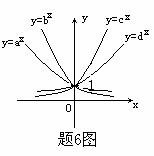
★6、指数函数y=ax,y=bx,y=cx,y=dx的图像如图所示,则a、b、c、d以及1之间的大小关系是:
A、a<b<1<c<d B、a<b<1<d<c
C、 b<a<1<d<c D、c<d<1<a<b
★7、设偶函数f(x)的定义域为R,当x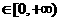 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f(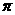 ),f(-3)的大小关系是:
),f(-3)的大小关系是:
A、f(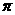 )>f(-3)>f(-2) B、f(
)>f(-3)>f(-2) B、f(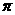 )>f(-2)>f(-3)
)>f(-2)>f(-3)
C、f(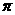 )<f(-3)<f(-2) D、f(
)<f(-3)<f(-2) D、f(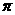 )<f(-2)<f(-3)
)<f(-2)<f(-3)
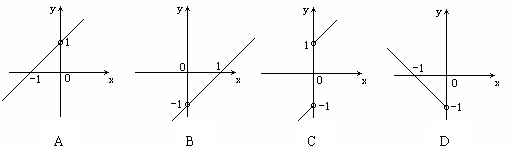 ★8、函数
★8、函数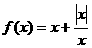 的图象是:
的图象是:
★9、函数y=x2+4x+5(其中x∈[-3,1)的值域为:
A [2,10) B、[1,10) C、[2,10] D、[1,10]
★10、已知函数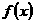 为R上的减函数,则满足
为R上的减函数,则满足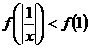 的实数
的实数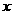 的取值范围是:
的取值范围是:
A.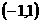 B.
B.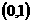 C.
C. 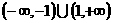 D.
D. 
●选择题答案
★16题、(1)、若半径为1的圆分别与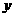 轴的正半轴和射线
轴的正半轴和射线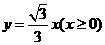 相切,求出这个圆的方程。
相切,求出这个圆的方程。
(2)、已知点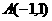 和圆
和圆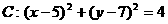 ,求一束光线从点A经x轴反射到圆周C的最短
路程。
,求一束光线从点A经x轴反射到圆周C的最短
路程。
★17题、(Ⅰ)、已知圆C的圆心坐标是(-1,3),且圆C与直线x+y-3=0相交于P,Q两点,又OP⊥OQ,O是坐标原点,求圆C的方程.
(Ⅱ)、已知⊙C满足:(1)、截y轴所得的弦长为2;(2)被x轴分成两段圆弧,其弧长之比为3:1;(3)、圆心到直线L:x-2y=0的距离为,求此圆的方程。
★ [题18]、(1)已知直线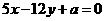 与圆
与圆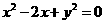 相切,求出
相切,求出 的值。
的值。
(2)、某条直线过点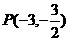 ,被圆
,被圆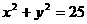 截得的弦长为8,求此弦所在的直线方程。
截得的弦长为8,求此弦所在的直线方程。
★[例题19]已知直线过点P(-1,2),且与以点A(-2,-3)、B(3,0)为端点的线段相交,求出直线L的斜率的取值范围是多少?
 ※★[题20]在平面直角坐标系中,已知矩形
※★[题20]在平面直角坐标系中,已知矩形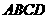 的长为2,宽为1,
的长为2,宽为1,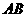 、
、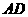 边分别在
边分别在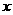 轴、
轴、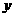 轴的正半轴上,
轴的正半轴上, 点与坐标原点重合(如图所示).将矩形折叠,使
点与坐标原点重合(如图所示).将矩形折叠,使 点落在线段
点落在线段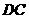 上.若折痕所在直线的斜率为
上.若折痕所在直线的斜率为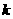 ,试写出折痕所在直线的方程。
,试写出折痕所在直线的方程。
★[题21]、已知圆C:(x-1)2+(y-2)2= 25,直线L:(2m+1)x+(m+1)y-7m-4=0;①证明;不论m取什么值,直线L恒与圆C相交于两点;②求直线被圆C所截得的弦长最小时,直线L的方程是什么?
★[题11]已知两条直线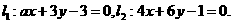 若
若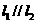 ,则
,则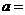
★[题12]已知圆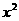 -4
-4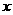 -4+
-4+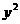 =0的圆心是点P,则点P到直线
=0的圆心是点P,则点P到直线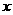 -
-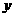 -1=0的距离是
-1=0的距离是
★[题13]圆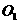 是以
是以 为半径的球
为半径的球 的小圆,若圆
的小圆,若圆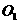 的面积
的面积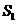 和球
和球 的表面积
的表面积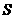 的比为
的比为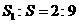 ,则圆心
,则圆心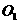 到球心
到球心 的距离与球半径的比
的距离与球半径的比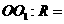 ____
____
★[题14]、若直线x+y=k与曲线y=恰有一个公共点,则k的取值范围是____
★[题15]、过点(1,)的直线L将圆(x-2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时,直线L的斜率k= .
|
题次 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
|
|
|
|
|
|
|
|
|
|
★答案:
★11.__________________; ★12题 :_____________;
★13题:__________________; ★14题:__________________; ★15题:________________
★[题1]、已知两条直线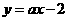 和
和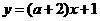 互相垂直,则
互相垂直,则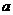 等于
等于
(A)2 (B)1 (C)0 (D)
★[题2]、已知过点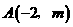 和
和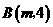 的直线与直线
的直线与直线 平行,则的值为
平行,则的值为
A  B
B 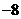 C
C 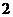 D
D 
★[题3]、经过点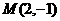 作圆
作圆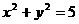 的切线,则切线的方程为:
的切线,则切线的方程为:
A. 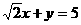 B.
B. 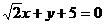 C.
C.  D.
D. 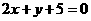
★4、圆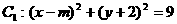 与圆
与圆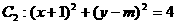 外切,则m的值为:
外切,则m的值为:
A. 2 B. -5 C. 2或-5 D. 不确定
★5、圆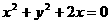 和
和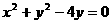 的公共弦所在直线方程为
的公共弦所在直线方程为
A. x-2y=0 B. x+2y=0 C. 2x-y=0 D. 2x+y=0
★6、直线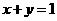 与圆
与圆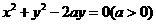 没有公共点,则
没有公共点,则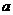 的取值范围是
的取值范围是
A.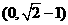 B.
B.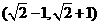 C.
C.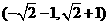 D.
D.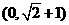
★[题7]、圆 上的点到直线
上的点到直线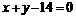 的最大距离与最小距离的差是
的最大距离与最小距离的差是
A.36
B. 18 C. 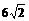 D.
D. 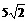
★[题8]设直线过点(0,a),其斜率为1, 且与圆x2+y2=2相切,则a 的值为
A.± B.±2 B.±2 D.±4
★[题9]、已知两定点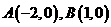 ,如果动点
,如果动点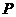 满足
满足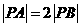 ,则点
,则点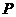 的轨迹所包围的图形的面积等于( ) A
的轨迹所包围的图形的面积等于( ) A 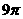 (B)
(B)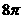 (C)
(C)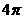 (D)
(D)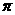
★[题10]、如果直线L将圆:x2+y2-2x-4y=0平分且不通过第四象限,则直线L的斜率的取值范围是
A [0,2] B [0,1] C [0, ] D [0, )
20.(I)(8分)甲乙两人约定在6时到7时在某地会面,并约定先到者等候另一人一刻钟,过时
即可离去,求两人能会面的概率?
(Ⅱ)(9分) 在120个零件中,一级品24个,二级品36个,三级品60个,从中抽取一个容量
为20的一个样本,求 ① 每个个体被抽到的概率,
② 若有简单随机抽样方法抽取时,其中个体α第15次被抽到的的概率,
③ 若用分层抽抽样样方法抽取时其中一级品中的每个个体被抽到的概率.
21(10分)、是否存在常数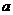 ,使得函数
,使得函数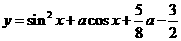 在闭区间[0,
在闭区间[0,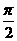 ]上的最大值是1?
]上的最大值是1?
若存在,求出对应的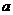 值;若不存在,试说明理由.
值;若不存在,试说明理由.
15、已知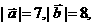
 与
与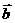 的夹角为
的夹角为 ,且
,且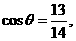 则
则 与
与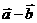 的夹角的余弦值为______
的夹角的余弦值为______
三:解答题:
16题(4+4+3+3=14分).函数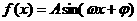
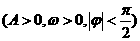 一段图象如图所示。
一段图象如图所示。
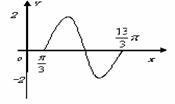 ⑴、求出函数
⑴、求出函数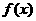 的解析式; (2)函数
的解析式; (2)函数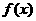 的图像可由函数y=sinx的图像经过怎样的平移和伸缩变换而得到? (3)、求出
的图像可由函数y=sinx的图像经过怎样的平移和伸缩变换而得到? (3)、求出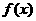 的单调递增区间;
的单调递增区间;
(4)、指出当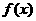 取得最小值时
取得最小值时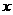 的集合.
的集合.
17(12分)、盒中有6只灯泡,其中2只次品,4只正品,有放回的从中任抽2次,每次抽取1只,试求下列事件的概率: (1)第1次抽到的是次品; (2)抽到的2次中,正品、次品各一次
18(10分).为了参加奥运会,对自行车运动员甲、乙两人在相同的条件下进行了6次测试,测得他们的最大速度的数据如表所示:
|
甲 |
27 |
38 |
30 |
37 |
35 |
31 |
|
乙 |
33 |
29 |
38 |
34 |
28 |
36 |
请判断:谁参加这项重大比赛更合适,并阐述理由。
19(12分). 设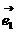 ,
,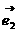 是两个不共线的非零向量,如果
是两个不共线的非零向量,如果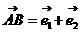 ,
,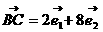 ,
,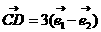 .
.
(1)、试确定实数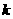 的值,使
的值,使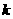 的取值满足向量
的取值满足向量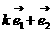 与向量
与向量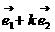 共线;
共线;
(2)、证明:A、B、D三点共线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com