
题目列表(包括答案和解析)
1、书本P5:练习题1;P11:习题1.1:题1、2、5:①②
1、 元素:用小写的字母a,b,c,…表示;元素之间用逗号隔开。
集合:用大写字母A,B,C,…表示;元素与集合的关系:∈、Ï
②、特殊的集合:N、Z、Q、R;N*、Æ;
③、集合中的元素具有确定性、互异性、无序性:
★[例题1]、已知集合A={a-2,2a2+5a,10},又-3∈A,求出a之值。
●解析:分类讨论思想;a=-1(舍去),a=
▲★课堂练习:
(17)(本小题满分9分)
设等差数列{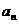 }的前
}的前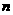 项和为
项和为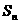 ,已知
,已知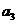 =
=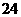 ,
, .
.
(Ⅰ) 求数列{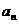 }的通项公式;
}的通项公式;
(Ⅱ)求数列{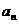 }的前n项和
}的前n项和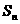 ;
;
(Ⅲ)当n为何值时,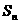 最大,并求
最大,并求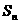 的最大值.
的最大值.
(18)(本小题满分9分)
 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=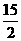 ,求AB的长.
,求AB的长.
(19)(本小题满分9分)
某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
(20)(本小题满分9分)
已知集合A=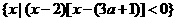 ,B=(2a,a2+1).
,B=(2a,a2+1).
(Ⅰ)当a=2时,求A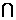 B;
B;
(Ⅱ)求使B  A的实数a的取值范围.
A的实数a的取值范围.
(11)在等差数列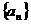 中,已知
中,已知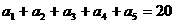 ,那么
,那么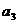 等于
.
等于
.
(12)已知在等比数列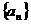 中,各项均为正数,且
中,各项均为正数,且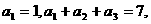 则数列
则数列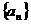 的通项公式是
的通项公式是 ;前n项和
;前n项和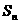 =
.
=
.
(13)在△ABC中,B=135°,C=15°,a=5,则此三角形的最大边长为 .
(14)已知△ABC的周长为9,且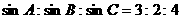 ,则cosC=
.
,则cosC=
.
(15)如果一个一元二次不等式的解集为(2,3),则这样的一元二次不等式可以是
(写出一个符合条件的不等式即可).
(16)关于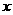 的不等式
的不等式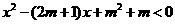 的解集为
.
的解集为
.
(1)已知数列{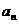 }的通项公式是
}的通项公式是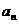 =
=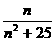 (
(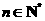 ),则数列的第5项为( )
),则数列的第5项为( )
(A)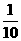 (B)
(B)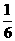 (C)
(C)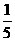 (D)
(D)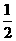
(2)数列1,3,6,10,…的一个通项公式an= ( )
(A)n2-n+1 (B)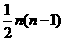 (C)
(C)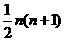 (D)
(D)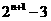
(3)数列{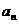 }的通项公式是
}的通项公式是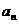 =
=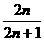 (
(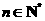 ),那么
),那么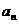 与
与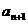 的大小关系是( )
的大小关系是( )
(A)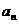 >
>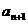 (B)
(B)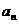 <
<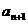
(C)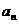 =
= 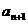 (D)不能确定
(D)不能确定
(4)某厂在1995年底制定生产计划,要使2005年底的总产量在1995年底的基础上翻两番,则年平均增长率为( )
(A)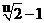 (B)
(B)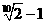 (C)
(C)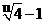 (D)
(D)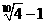
(5)在△ABC中,若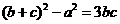 ,则角A=( )
,则角A=( )
(A)30° (B)60° (C)120° (D)150°
(6)在△ABC中,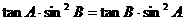 ,那么△ABC一定是( )
,那么△ABC一定是( )
(A)锐角三角形 (B)直角三角形
(C)等腰三角形 (D)等腰三角形或直角三角形
(7)若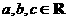 ,且
,且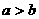 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
(A)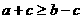 (B)
(B)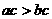
(C)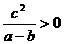 (D)
(D)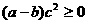
(8)不等式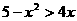 的解集为( )
的解集为( )
(A)(-5,1) (B)(-1,5)
(C)(-∞,-5)∪(1,+∞) (D)(-∞,-1)∪(5,+∞)
(9)若0<a<1,0<b<1,把a+b,2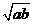 ,2ab中最大与最小者分别记为M和m,则(
)
,2ab中最大与最小者分别记为M和m,则(
)
(A)M=a+b, m=2ab (B)M=2ab, m=2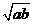
(C)M=a+b, m=2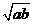 (D)M=2
(D)M=2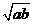 , m=2ab
, m=2ab
(10)设x>0,y>0,x+y+xy=2,则x+y的最小值是( ) (A) (B)1 + (C)2-2 (D)2-
16、(10分)正四棱台(上、下底面均为正方形的四棱台)的侧棱长为3cm,两底面边长分别为1cm和5cm,画出其三视图,并求出其表面积和体积
17(14分).(1)、求经过直线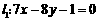 和
和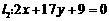 的交点,且垂直于直线
的交点,且垂直于直线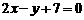 的直线方程.
的直线方程.
(2)、直线l经过点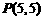 ,且和圆C:
,且和圆C: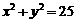 相交,截得弦长为
相交,截得弦长为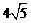 ,求l的方程.
,求l的方程.
18(12分).已知幂函数y=x3-p(p∈N*)的图象关于y轴对称,且在(0,+∞)上为增函数,求满足条件(a+1)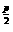 <(3-2a)
<(3-2a)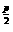 的实数a的取值范围。
的实数a的取值范围。
19(12分).某飞机制造公司一年中最多可生产某种型号的飞机100架。已知制造x架该种飞机的产值函数为R(x)=3000x-20x2 (单位:万元),成本函数C(x)=500x+4000 (单位:万元)。利润是收入与成本之差,又在经济学中,函数¦(x)的边际利润函数M¦x)定义为:M¦x)=¦(x+1)-¦(x).
①、求利润函数P(x)及边际利润函数MP(x);(利润=产值-成本)
②、问该公司的利润函数P(x)与边际利润函数MP(x)是否具有相等的最大值?
20(14分).如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明 PA//平面EDB;
(2)证明PB⊥平面EFD;
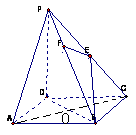 (3)求二面角C-PB-D的大小.
(3)求二面角C-PB-D的大小.
21(13分).若非零函数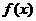 对任意实数
对任意实数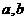 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当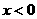 时,
时,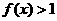 .
.
(1)求证: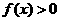 ;
;
(2)求证: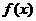 为减函数;
为减函数;
(3)当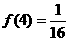 时,解不等式
时,解不等式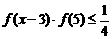
13题:__________________; 14题:__________________; 15题:________________
|
题次 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
|
|
|
|
|
|
|
|
|
|
15、在圆 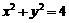 上,与直线4x+3y-12=0的距离最小的点的坐标
.
上,与直线4x+3y-12=0的距离最小的点的坐标
.
14、已知l⊥α,m β,则下面四个命题:
β,则下面四个命题:
①α∥β则l⊥m ②α⊥β则l∥m ③l∥m则α⊥β ④l⊥m则α∥β
其中正确的是________ ( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com