
题目列表(包括答案和解析)
(二)、含有n个元素的集合A的子集个数是_____2n,,真子集个数是___2n-1,非空真子集:2n-2
★[例题1]、已知集合P={x|x2-5x+4≤0},Q={x|x2-(b+2)x+2b≤0}且有PÊQ,求实数b的取值范围。
●解:{b|1≤b≤4};注意利用数轴去加以判断。
★[例题2]、(2007年湖南·10题).设集合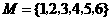 ,
,  都是
都是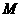 的含两个元素的子集,且满足:对任意的
的含两个元素的子集,且满足:对任意的 ,
,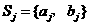 (
(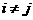 ,
,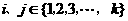 ),都有
),都有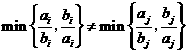 (
(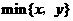 表示两个数
表示两个数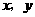 中的较小者),则
中的较小者),则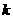 的最大值是( B
)
的最大值是( B
)
A.10 B.11 C.12 D.13
★[例题3]、(2007年北京文科·15题·12分)记关于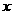 的不等式
的不等式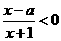 的解集为
的解集为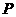 ,不等式
,不等式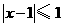 的解集为
的解集为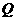 .
.
(I)若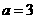 ,求
,求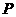 ; (II)若
; (II)若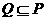 ,求正数
,求正数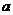 的取值范围.
的取值范围.
●解:(I)由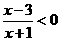 ,得
,得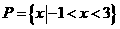 .
.
(II)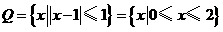 .
.
由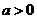 ,得
,得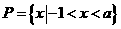 ,又
,又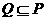 ,所以
,所以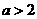 ,即
,即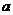 的取值范围是
的取值范围是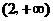 .
.
▲★课堂练习:
1、书本P7:练习题1、2、3;P12: 5:①②③;B组第2题。
2、已知集合A={2,8,a}, B={2,a2-3a+4},又AÝB,求出a之值。(解:a= -1或4)
3、已知集合A={x|-3≤x≤4}B={x|2m-1≤x≤m+1},当BÍA时,求出m之取值范围。(解:m≥-1)
特别注意:当BÍA时,B一定包括有两种情形:B=Æ或B≠Æ,解题时极易漏掉B=Æ这一情况从而出错!
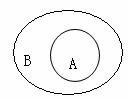
(一)、集合之间的基本关系:子集Í、真子集Ü、空集Æ(如方程x2+1=0的根);集合的相等。
★[题1]、(2006年Æ·辽宁·T5·5分)设⊕是R上的一个运算,A是R上的非空子集,若对任意的a、b∈A,有a⊕b∈A,则称A对运算⊕封闭,下列数集对加法、减法、乘法和除法(除数不等于0)四则运算都封闭的是( C )
A 自然数集 B 整数集 C 有理数集 D 无理数集
★[题2](2006年·山东·T1·5分)定义集合运算:A⊙B={z︳z= xy(x+y),z∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为( D )
(A)0 (B)6 (C)12 (D)18
★[题3](2005年·湖北·T1·5分)设P、Q为两个非空实数集合,定义集合P+Q=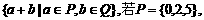
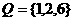 ,则P+Q中元素的个数是( B )
,则P+Q中元素的个数是( B )
A.9 B.8 C.7 D.6
★[题4](广东2007年理科·8题)设 是至少含有两个元素的集合,在
是至少含有两个元素的集合,在 上定义了一个二元运算“*”(即对任意的
上定义了一个二元运算“*”(即对任意的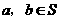 ,对于有序元素对(
,对于有序元素对(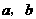 ),在
),在 中有唯一确定的元素
中有唯一确定的元素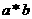 与之对应).若对任意的
与之对应).若对任意的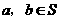 ,有
,有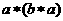
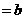 ,则对任意的
,则对任意的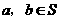 ,下列等式中不恒成立的是( A )
,下列等式中不恒成立的是( A )
A.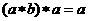 B.
B.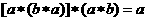
C.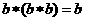 D.
D.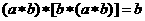
(Ⅲ)、课堂回顾与小结:
1、 记准N、Z、Q、R;Æ
2、 分清列举法和描述法,注意集合中的元素是否满足互异。Æ◆Ü÷
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义二: 集合之间的基本关系(2课时)
 撰稿:
方锦昌 电子邮箱 fangjingchang2 007@ 手机号码 13975987411
撰稿:
方锦昌 电子邮箱 fangjingchang2 007@ 手机号码 13975987411
(Ⅰ)、基本概念及知识体系:
1、集合之间的基本关系:包含关系------子集Í、真子集Ü、空集Æ;集合的相等。
2、注意韦恩图、利用数轴的数形结合思想以及分类讨论的数学思想的培养与应用。
(Ⅱ)、典例剖析与课堂讲授过程:
3、已知集合N={∈Z | x∈N},求出集合N。(解:N={1,2,3,6}
2、已知集合M={x∈N|∈Z},求出集合M。(解:M={0,1,2,5}
1、已知集合B={x|ax2-3x+2=0,a∈R},若B中的元素至多只有一个,求出a的取值范围。(解:a=0或a≥9/8)
2、设集合M={x|x= 4m+2,m∈Z},N={y|y= 4n+3,n∈Z},若x0∈M,y0∈N,则x0·y0与集合M、N的关系是( A):A、x0·y0∈M B、x0·y0ÏM C、x0·y0∈N D、无法确定
●解:x0·y0= 4(4mn+3m+2n+1)+2,则x0·y0∈M
★[例题2]、书本P3:例题1、P4:例题2
★[例题3]、已知下列集合:(1)、 ={n | n = 2k+1,k
={n | n = 2k+1,k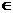 N,k
N,k 5};(2)、
5};(2)、 ={x | x = 2k, k
={x | x = 2k, k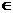 N, k
N, k 3};(3)、
3};(3)、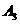 ={x | x = 4k+1,或x = 4k-1,k
={x | x = 4k+1,或x = 4k-1,k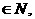 k
k 3};
3};
问:(Ⅰ)、用列举法表示上述各集合;(Ⅱ)、对集合 ,
, ,
,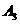 ,如果使k
,如果使k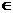 Z,那么
Z,那么 ,
, ,
,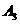 所表示的集合分别是什么?并说明
所表示的集合分别是什么?并说明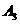 与
与 的关系。
的关系。
●
解:(Ⅰ)、⑴  ={n
| n = 2k+1,k
={n
| n = 2k+1,k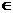 N ,k
N ,k 5}={1,3,5,7,9,11};
5}={1,3,5,7,9,11};
⑵、 ={x | x = 2k, k
={x | x = 2k, k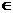 N, k
N, k 3}={0,2,4,6};
3}={0,2,4,6};
⑶、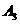 ={x | x = 4k
={x | x = 4k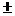 1,k
1,k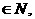 k
k 3}={-1,1,3,5,7,9,11,13};
3}={-1,1,3,5,7,9,11,13};
(Ⅱ)、对集合 ,
, ,
,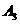 ,如果使k
,如果使k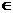 Z,那么
Z,那么 、
、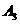 所表示的集合都是奇数集;
所表示的集合都是奇数集; 所表示的集合都是偶数集。
所表示的集合都是偶数集。
▲点评:(1)通过对上述集合的识别,进一步巩固对描述法中代表元素及其性质的表述的理解;
(2)掌握奇数集.偶数集的描述法表示和集合的图示法表示。
★[例题4]、已知某数集A满足条件:若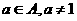 ,则
,则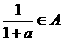 .
.
①、若2 ,则在A中还有两个元素是什么;②、若A为单元素集,求出A和
,则在A中还有两个元素是什么;②、若A为单元素集,求出A和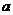 之值.
之值.
● 解:①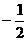 和
和 ; ②
; ②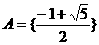 (此时
(此时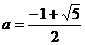 )或
)或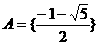 (此时
(此时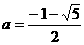 )。
)。
▲●课堂练习:
1、书本P5:练习题2;P12:题3、4
3、已知集合A={a+2,(a+1)2,a2+3a+3},又1∈A,求出a之值。(解:a=0)
2、已知集合A={1,0,x},又x2∈A,求出x之值。(解:x=-1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com