
题目列表(包括答案和解析)
(四)、提高练习:
★[题1]、已知函数f (x)=2x-1,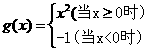 ,求f[g(x)]和g[f(x)]之值。
,求f[g(x)]和g[f(x)]之值。
★[题2]、书本:P25:6题。
★[题3]、已知函数f(x+1)=x2-3x+2,求f(x)之表达式
★[题4]、已知函数f(+4)=x+8+2,求f(x2)之表达式(学习高手P44)
★思考题:[题5]、二次函数¦(x)=ax2+bx (a,b为常数且a≠0)满足¦(-x+5)=¦(x-3)且方程¦(x)=x有等根;①求¦(x)的解析式;②是否存在实数m、n(m <n)使¦(x)定义域为[m,n],值域为[3m,3n],若存在,求出m、n之值,若不存在,说明理由
解、①¦(x)=-x2+x ②由于¦(x)的值域是¦(x)≤,则3n≤,即n≤,所以有¦(m)=3m且¦(n)=3n
∴存在实数m=-4,n=0使¦(x)定义域为[-4,0],值域为[-12,0]
(Ⅲ)、课堂回顾与小结:
1、注意函数的表示和定义域问题。
2.已知函数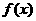 ,
,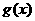 分别由下表给出
分别由下表给出
 |
1 |
2 |
3 |
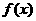 |
1 |
3 |
1 |
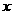 |
1 |
2 |
3 |
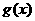 |
3 |
2 |
1 |
则
则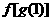 的值
的值
为 ;满足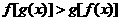 的
的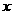 的值是 2.
的值是 2.
3.设函数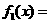
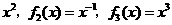 ,则
,则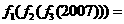 .
.
4、已知a,b为常数,若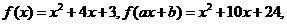 则
则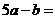 2 .
2 .
5.函数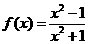 , 则
, 则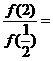 ( B )
( B )
A.2 B.-2 C.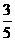 D.
D.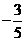
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义五: 函数及其表示(2)
撰稿: 方锦昌 电子邮箱 fangjingchang2007@ 手机号码 13975987411
(Ⅰ)、基本概念及知识体系:
函数的概念、函数的定义域、值域,注意充分利用函数的图象,培养基本的数形结合的思想方法。
[★例题1]设¦(x+1)的定义域为[-2,3)则¦(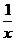 +2)的定义域为___({x|x≤或x>}
+2)的定义域为___({x|x≤或x>}
[★例题2]、将进货单价为80元的商品400个,按90元一个售出时全部卖出,已知这种商品每个涨价1元,其销售个数就减少20个,为了获得最大利润,售价应定为每个多少元。
★●练习题:
1、下面可能表示函数的图象的是( )

★1、(07广东)客车从甲地以60km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,最后到达丙地所经过的路程s与时间t之间关系的图象中,正确的是( )
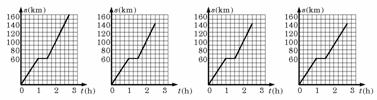
A. B. C. D. B.
(Ⅱ)、典例剖析与课堂讲授过程:
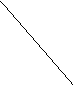
●例题1:(2000年全国高考题)某种蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价p与上市时间t的关系图是一条折线(如图(1)),种植成本Q与上市时间t的关系是一条抛物线(如图(2))①、写出西红柿的市场售价与时间的函数解析式p=f(t).
②、写出西红柿的种植成本与时间的函数解析式Q=g(t).
③、认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
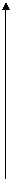
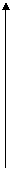
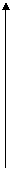 p
Q
p
Q




 300
300
300
300
 250
250




 200
200
200
200



 150
150





 100
100
100
100









 50
50

 O 100 200
300 t
O 50 100 150 200 250 300 t
O 100 200
300 t
O 50 100 150 200 250 300 t
(图1) (图2)
●解:(1)f(t)=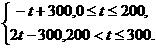
(2)g(t)=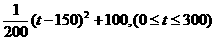 .
.
(3)纯收益h(t)=f(t)-g(t)
=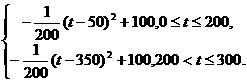
当t=50时,h(t)的最大值为100,即从2月1日开始的第50天西红柿的纯收益最大.
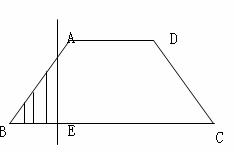 ★[题2]如右图,已知底角45º为的等腰梯形ABCD,底边BC长为7,腰长为
★[题2]如右图,已知底角45º为的等腰梯形ABCD,底边BC长为7,腰长为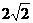 ,当一条垂直于底边BC(垂足为E)的直线
,当一条垂直于底边BC(垂足为E)的直线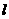 从左至右移动(与梯形ABCD有公共点)时,直线
从左至右移动(与梯形ABCD有公共点)时,直线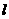 把梯形分成两部分,令BE=x,试写出图中阴影部分的面积y与x的函数关系式.
把梯形分成两部分,令BE=x,试写出图中阴影部分的面积y与x的函数关系式.
解: 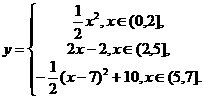
●[题3]、有一种密英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不分大小写),依次对应1,2,3,…,26这26个自然数,见如下表格:
|
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
给出如下一个的变换公式:
 x′= (x∈N,1≤x≤26,x不能被2整除)
x′= (x∈N,1≤x≤26,x不能被2整除)
+13(x∈N,1≤x≤26,x能被2整除) 将明文转换成密文,如8→+13=17,即h变成q;5→=3,即e变成c。①按上述规定,将明文good译成的密文是什么?②按上述规定,若将某明文译成的密文是shxc,那么原来的明文是什么?
●解:①g→7→=4→d;o→15→=8→h;d→o;则明文good的密文为dhho
 ②逆变换公式为x= 2x′-1 (x′∈N, 1≤x′≤13)
②逆变换公式为x= 2x′-1 (x′∈N, 1≤x′≤13)
2x′-26 (x′∈N,14≤x′≤26),则有s→19→2×19-26=12→l;h→8→2×8-1=15→o,x→24→2×24-26=22→v;c→3→2×3-1=5→e;故密文shxc的明文为love.
 四、今日作业:
四、今日作业:
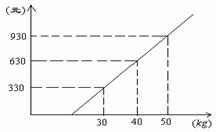
★1、.某航空公司规定,乘机所携带行李的重量(kg)
与其运费(元)由如图的一次函数图像确定,那
么乘客免费可携带行李的最大重量为 ______
_____19 kg _.
★2.某校校长暑假将带领该校市级“三好生”去北京旅游。甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优待。”乙旅行社说:“包括校长在内,全部按全票价的6折(即按全票价的60%收费)优惠。”若全票价为240元.;(I)设学生数为x,甲旅行社收费为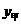 ,乙旅行社收费为
,乙旅行社收费为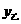 ,分别计算两家旅行社的收费(建立表达式);(II)当学生数是多少时,两家旅行社的收费一样;(III)就学生数x讨论哪家旅行社更优惠.
,分别计算两家旅行社的收费(建立表达式);(II)当学生数是多少时,两家旅行社的收费一样;(III)就学生数x讨论哪家旅行社更优惠.
★解:(I)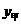 =120x+240,
=120x+240, 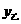 =240·60%(x+1)=144x+144.
=240·60%(x+1)=144x+144.
(II)根据题意,得120x+240=144x+144, 解得 x=4.
答:当学生人数为4人时,两家旅行社的收费一样多.
(III)当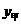 >
>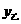 ,120x+240>144x+144, 解得 x<4;
,120x+240>144x+144, 解得 x<4;
当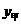 <
<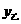 , 120x+240<144x+144, 解得 x>4.
, 120x+240<144x+144, 解得 x>4.
答:当学生人数少于4人时,乙旅行社更优惠;当学生人数多于4人时,甲旅行社更优惠.
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义六: 函数的值域和映射概念
撰稿: 方锦昌 电子邮箱 fangjingchang2007@ 手机号码 13975987411
(Ⅰ)、基本概念及知识体系:
函数的概念、函数的定义域、值域,注意充分利用函数的图象,培养基本的数形结合的思想方法。
[★例题1]
■①、设¦(x+1)的定义域为[-2,3)则¦(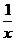 +2)的定义域为___({x|x≤或x>}
+2)的定义域为___({x|x≤或x>}
■②、求下列函数的定义域(用区间表示)
f(x)=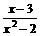 ; f(x)=
; f(x)= ; f(x)=
; f(x)=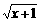 -
-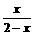
(Ⅱ)、教学:函数值域的求法:
1、常见函数的值域:①、一次函数y= kx+b (k≠0)的值域: ②、二次函数y= ax2+bx+c (a≠0)的值域: ③、反比例函数y= (k≠0)的值域:
●例2:求值域(用区间表示):y=x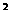 -2x+4;f(x)=;y=
-2x+4;f(x)=;y=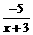 ;f(x)=
;f(x)=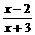 ;
;
▲★:小结求值域的方法: 观察法、配方法、拆分法、基本函数法
(Ⅲ)、巩固练习:
▲1、求下列函数的值域:
①、y= 4-:配方及图象法: ②、y=+x的值域 (换元法答案:y≤1); ③、y= 分离常数法: ④、y= 判别式法或均值不等式法:
●2.求函数y=-x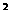 +4x-1 ,x∈[-1,3) 在值域。
+4x-1 ,x∈[-1,3) 在值域。
解、(数形结合法):画出二次函数图像 → 找出区间 → 观察值域(注意描成阴影部分)
◆3.已知函数f(x)的定义域是[0,1],则函数f(x+a)的定义域是 。
#●4.课堂作业:书P24: 1、2、3题。
(Ⅳ)、综合提高部分:
[★例题1]设函数¦(x)=x2-2x+2,x∈[t,t+1]的最小值为g(t),写出g(t)的表达式。
解:注意利用图形去处理问题,培养一种数形结合的思想方法.
[★题2] 设函数¦(x)表示-2x+2与-2x2 +4x+2中的最小值,则¦(x)的最大值为( B )
A 1 B 2 C 3 D 0
(Ⅴ)、典例剖析与课堂讲授:
●★[例题3]、二次函数¦(x)=ax2+bx(a,b为常数且a≠0)满足¦(-x+5)=¦(x-3)且方程¦(x)=x有等根;①求¦(x)的解析式;②是否存在实数m、n(m <n)使¦(x)定义域为[m,n],值域为[3m,3n],若存在,求出m、n之值,若不存在,说明理由
▲解、①¦(x)= -x2+x ②由于¦(x)的值域是¦(x)≤,则3n≤,即n≤,所以有¦(m)=3m且¦(n)=3n ∴存在实数m=-4,n=0使¦(x)定义域为[-4,0],值域为[-12,0]
●注意:若函数满足有:¦(a+x)=¦(b-x)则此函数必有对称轴:x=
(Ⅵ). 教学映射概念:
① 先看几个例子,两个集合A、B的元素之间的一些对应关系,并用图示意
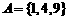 ,
, 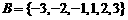 ,对应法则:开平方;
,对应法则:开平方;
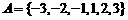 ,
,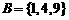 ,对应法则:平方;
,对应法则:平方;
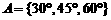 ,
, 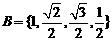 , 对应法则:求正弦;
, 对应法则:求正弦;
② 定义映射:一般地,设A、B是两个非空的集合,如果按某一个确定的对应法则f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称对应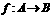 为从集合A到集合B的一个映射(mapping).记作“
为从集合A到集合B的一个映射(mapping).记作“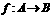 ”
”
关键: A中任意,B中唯一;对应法则f.
口诀:看原象,要求每元必有象,且象唯一。对应方式:一对一;多对一;不允许一对多!
2.教学例题:
① 出示书本例题7: 探究从集合A到集合B一些对应法则,哪些是映射,哪些是一一映射?
A={P | P是数轴上的点},B=R; A={三角形},B={圆};
A={ P | P是平面直角体系中的点}, 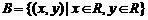 ; A={高一某班学生},B= ?
; A={高一某班学生},B= ?
③ 练习:判断下列两个对应是否是集合A到集合B的映射?
A={1,2,3,4},B={3,4,5,6,7,8,9},对应法则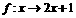 ;
;
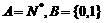 ,对应法则
,对应法则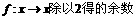 ;
;
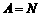 ,
,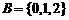 ,
,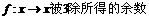 ;
;
设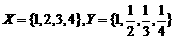
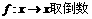 ;
;
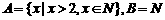 ,
,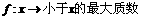
(三)、今日作业:
●1、设f(x)=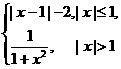 ,则f[f(
,则f[f(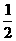 )]=( B )
)]=( B )
(A) 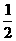 (B)
(B)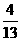 (C)-
(C)-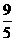 (D)
(D) 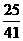
解:f[f(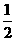 )]=f[|
)]=f[|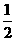 -1|-2]=f[-
-1|-2]=f[-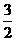 ]=
]=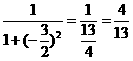 ,选(B)
,选(B)
(二)、函数的定义域的常见求法:
★[例题1]、书本P17例题1、例题2
★[例题2]、如果函数¦(x)满足:对任意的实数m、n都有¦(m)+ ¦(n)= ¦(m+n)且¦(1003)=2,则¦(1)+ ¦(3)+ ¦(5)+…+¦(2005)=____(2006)
★[例题3]、(06·重庆·T21·12分)已知定义域为R的函数f(x)满足¦(f(x)-x2+x)=f(x)-x2+x.
(Ⅰ)若f(2)=3,求f(1);又若f(0)=a,求f(a);(Ⅱ)设有且仅有一个实数x0,使得f(x0)= x0,求函数f(x)的解析表达式.
▲解:(Ⅰ)因为对任意x∈R,有f(f(x)- x2 + x)=f(x)- x2 +x,所以f(f(2)- 22+2)=f(2)- 22+2.
又由f(2)=3,得f(3-22+2)-3-22+2,即f(1)=1.;若f(0)=a,则f(a-02+0)=a-02+0,即f(a)=a.
(Ⅱ)因为对任意xεR,有f(f(x))- x2 +x)=f(x)- x2 +x.;又因为有且只有一个实数x0,使得f(x0)- x0.
所以对任意x∈R,有f(x)- x2
+x= x0.;在上式中令x= x0,有f(x0)-x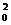 + x0= x0,
+ x0= x0,
又因为f(x0)- x0,所以x0- x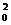 =0,故x0=0或x0=1.;若x0=0,则f(x)- x2 +x=0,即f(x)= x2 –x.
=0,故x0=0或x0=1.;若x0=0,则f(x)- x2 +x=0,即f(x)= x2 –x.
但方程x2 –x=x有两上不同实根,与题设条件矛质,故x2≠0.
若x2=1,则有f(x)- x2 +x=1,即f(x)= x2 –x+1.易验证该函数满足题设条件.
综上,所求函数为f(x)= x2 –x+1(x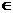 R).
R).
▲★课堂练习:
●练习题:书本P19题1、2、3;书本P24:习题1、2、3、4、5
●思考题:已知函数¦(x)对一切实数x、y均有¦(x+y)-¦(y)=(x+2y+1)·x成立,且¦(1)=0
①求¦(0)之值;②当¦(x)+3<2x+a 且0<x< 恒成立时,求a的取值范围
解、①¦(0)=-2; ②化为a>(x-)2+从而有{a| a≥1}为所求(函数的恒成立问题--函数思想去处理!)
(一)、函数的概念:
(四)、提高练习:
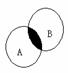
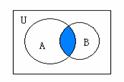 ●★[题1]、设全集U=R,A={x| <0},B={x|x<-1},则图中阴影部分所表示的集合是( C )
●★[题1]、设全集U=R,A={x| <0},B={x|x<-1},则图中阴影部分所表示的集合是( C )
A {x|x>0} B {x|-3<x<0} C {x|-3<x<-1} D {x|x<-1}
●★[题2]、集合A={(x,y)|2x+y=5,x∈N,y∈N},则A的非空真子集的个数为(C )
A 4 B 5 C 6 D 7
★[题3]、集合M={x||x-3|≤4},N={y|y= +},则M∩N=____{0}
★[题4]、(2004年·上海·T3·4分)设集合A={5,log2(a+3)},集合B={a,b}若满足A∩B={2},则A∪B=____{1,2,5}
★ [题5]、①已知集合A={y|y=},B={y|y=x2-2x-3,x∈R},则A∩B=____{y|y≥0}
②已知集合A={x|y=},B={y|y=x2-2x-3,x∈R},则A∩B=____{x|x≥1或≤x≤}
★[题6]、已知集合P={x|x2-5x+4≤0},Q={x|x2-(b+2)x+2b≤0}且有PÊQ,求实数b的取值范围。
解:(答案:{b|1≤b≤4})
 ★[题7]、若全集I=R,¦(x),g(x)均为x的二次函数,且P={x|¦(x)<0},Q={x| g(x)≥0,}则不等式组
★[题7]、若全集I=R,¦(x),g(x)均为x的二次函数,且P={x|¦(x)<0},Q={x| g(x)≥0,}则不等式组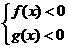 的解集可用P、Q表示为___( P∩CRQ)
的解集可用P、Q表示为___( P∩CRQ)
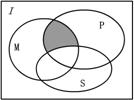
★[题8]、.如右图所示,I为全集,M、P、S为I的子集,则阴影部分所表示的集合为( C )
A.(M∩P)∪S B.(M∩P)∩S
C.(M∩P)∩(CI S) D.(M∩P)∪(CI S)
●题9、(2007年江苏第2题).已知全集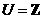 ,
,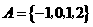 ,
,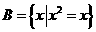 ,则A∩(CRB)为( A )
,则A∩(CRB)为( A )
A.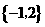 B.
B.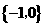 C.
C.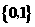 D.
D.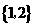
★题10、(07北京)已知集合 ,
,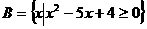 ,若
,若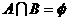 ,则实数
,则实数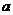 的取值范围是
.
的取值范围是
.
(Ⅲ)、课堂回顾与小结:
5、 注意集合之间的运算:交、并、补;
6、 利用韦恩图,利用数轴,注意分类讨论思想的培养与应用。
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义四: 函数及其表示(1)
撰稿: 方锦昌 电子邮箱 fangjingchang2 007@ 手机号码 13975987411
(Ⅰ)、基本概念及知识体系:
1、 函数概念:书本:P15实例1、炮弹的发射--解析法;实例2、臭氧问题--图象法;实例3、恩格尔系数--列表法;
2、 函数的定义:P16定义:设A、B是非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数 和它对应,那么称
和它对应,那么称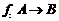 为从集合A到集合B的一个函数(function),记作:
为从集合A到集合B的一个函数(function),记作: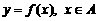 . 其中,x叫自变量,x的取值范围A叫作定义域(domain),与x的值对应的y值叫函数值,函数值的集合
. 其中,x叫自变量,x的取值范围A叫作定义域(domain),与x的值对应的y值叫函数值,函数值的集合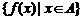 叫值域(range);注意记为y=f(x),x∈A;
叫值域(range);注意记为y=f(x),x∈A;
3、 构成函数的三要素是:定义域、值域、对应法则。
4、函数y=f(x)的定义域和值域:已学的一次函数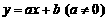 、二次函数
、二次函数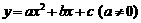 的定义域与值域?
的定义域与值域?
●练习:题1、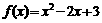 ,求f(0)、f(1)、f(2)、f(-1)的值。
,求f(0)、f(1)、f(2)、f(-1)的值。
→ 题2、求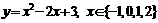 值域.
值域.
5、 区间的概念:
●练习:1、用区间表示:R、{x|x≥a}、{x|x>a}、{x|x≤b}、{x|x<b}
2、 用区间表示:函数y=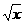 的定义域
,值域是 。
的定义域
,值域是 。
●作业: 已知函数f(x)=3x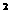 +5x-2,求f(3)、f(-
+5x-2,求f(3)、f(-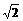 )、f(a)、f(a+1)
)、f(a)、f(a+1)
(Ⅱ)、典例剖析与课堂讲授过程:
(三)、今日作业:
●1、已知集合A={x|x+2>0},B={x|ax-3<0}且有A∪B=A,求a 的取值范围。 (解:{a|a≤-3/2})
●2、书本P12:10题、B组4题。
(二)、A∪B=A ⇔BÍA,要特别注意B是否为Æ的情况的讨论。
★[例题1]、已知集合A={x|x2-2x-8=0},B={x|x2+ax+a2-12=0}且有A∪B=A ,求实数a的取值集合。
●解:{a|a<-4,或a=-2,或a≥4};注意Æ,注意分类讨论。
★[例题2]、已知全集U={x|x≤4},集合A={x|-2<x<3}, 集合B={x|-3<x≤3},求①、CUA,②、A∩B,③、CU(A∩B),④、(CUA)∩B,⑤、CU(A∪B)
●解:{a|a<-4,或a=-2,或a≥4};注意Æ,注意分类讨论。
★[例题3]、已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},且有A∩B≠Æ,求实数m的取值范围。
●解:(正难则反,补集的思想){m|m≤-1}
▲★课堂练习:
◆1、书本P11:练习题1、2、3、4;P12: 6、7、8、9;B组第3、题。
◆2、、(2006年·辽宁·T1·5分)设集合A={1,2},则满足A∪B={1,2,3}的集合B的个数为( C )
A 1 B 3 C 4 D 8
◆3、(2005年·全国Ⅰ·T2·5分)设I为全集,S1、S2、S3是I 上的三个非空子集,且S1∪S2∪S3=I,则下列论断正确的是( C )
A CIS1∩(S2∪S3)=Æ B S1Í(CIS2∩CIS3) C CIS1∩CIS2∩CIS3=Æ D S1Í(CIS2∪CIS3)
◆ 4、已知集合A={x|-3≤x≤4}B={x|2m-1≤x≤m+1},当A∪B=A时,求出m之取值范围。
(解:m≥-1)
特别注意:当BÍA时,B一定包括有两种情形:B=Æ或B≠Æ,解题时极易漏掉B=Æ这一情况从而出错!
(一)、集合之间的基本运算:
A∩B={x|x∈A且x∈B}; A∪B={x|x∈A或x∈B};CUA={x|x∈U且xÏA}
(四)、提高练习:
★[题1]、设集合S={a,b,c,d,e},则包含{a,b}的S的子集共有(D )个
A 2 B 3 C 5 D 8
★[题2]、集合A={(x,y)|2x+y=5,x∈N,y∈N},则A的非空真子集的个数为(C )
A 4 B 5 C 6 D 7
★[题3]、对于两个非空数集A、B,定义点集如下:A×B={(x,y)|x∈A, y∈B},若A={1,3},B={2,4},则点集A×B的非空真子集的个数是___14_个
★[题4]、集合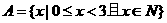 的真子集个数是 ( A )
的真子集个数是 ( A )
(A)16 (B)8 (C)7 (D)4
●解答、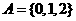 ,A的真子集有:
,A的真子集有: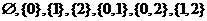 ,共7个,选C
,共7个,选C
★[题5]、(2004湖北)已知集合P={m|-1<m<0},Q={m∈R|mx2+4mx-4<0对任意的x∈R恒成立},则有( B )
A P=Q B PÜQ C PÝQ D P∩Q=Q
★[题6]、设集合M={x|x= +,k∈Z},N={x|x= +,k∈Z},则( B)
A M=N B MÜN C MÝN D M∩N=Æ
(Ⅲ)、课堂回顾与小结:
3、 分清子集Í、真子集Ü、空集Æ;注意Æ的特殊性。
4、 利用韦恩图,利用数轴,注意分类讨论思想的培养与应用。
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义三: 集合之间的基本运算(2课时)
撰稿: 方锦昌 电子邮箱 fangjingchang2 007@ 手机号码 13975987411
 (Ⅰ)、基本概念及知识体系:
(Ⅰ)、基本概念及知识体系:
1、
 集合之间的基本运算:①、交集A∩B={x|x∈A且x∈B};
集合之间的基本运算:①、交集A∩B={x|x∈A且x∈B};
②、并集A∪B={x|x∈A或x∈B};
③、全集和补集:CUA={x|x∈U且xÏA}
2、注意韦恩图、利用数轴的数形结合思想以及分类讨论的数学思想的培养与应用。
(Ⅱ)、典例剖析与课堂讲授过程:
(三)、今日作业:
●1、判断下列集合A与B之间有怎样的包含或相等关系:
①、已知集合A={x|x=2k-1,k∈Z}B={x|x=2m+1,m∈Z}(解:A=B)
②、已知集合A={x|x=2k,k∈Z}B={x|x=4m,m∈Z}(解:B Í A)
●2、已知集合M={x|-2≤x≤5},N={x|m+1≤x≤2m-1}
①、若NÍM,求实数m的取值范围;(解:m≤3,注意N为Æ的情况!)
②、若x∈Z,则M的非空真子集的个数是多少个?(解:28-2=254个)
③、(选做)当x∈R 时,没有元素使得x∈M与x∈N同时成立,求实数m的取值范围(解:m<2或m>4)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com