
题目列表(包括答案和解析)
1.指出函数f(x)=ax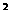 +bx+c (a>0)的单调区间及单调性,并进行证明。
+bx+c (a>0)的单调区间及单调性,并进行证明。
(一)、基本概念及知识体系:
教学要求:更进一步理解函数单调性的概念及证明方法、判别方法,理解函数的最大(小)值及其几何意义.
教学重点:熟练求函数的最大(小)值。
教学难点:理解函数的最大(小)值,能利用单调性求函数的最大(小)值。
教学过程:
★题1、已知函数f(x)= (x∈[2,+∞),证明该函数为↗,并求出其最小值。
解:(见教案P45面题2);(为)
★题2、已知函数f(x)=ax2-2ax+2+b(a≠0)在[2,3]上的最大值为5和最小值为2,求出a和b 之值。
●解:a=-1,b=3或a=1,b=0见教案P45面题1。
★题3、已知函数f(x)= x2+bx+c,对任意的实数t,都有f(2=t)=f(2-t),试比较f(1)、f(2)、f(4)之大小。
●解:见教材全解P108例题4;注意函数满足f(a+x)=f(b-x)时,其对称轴为x=a+b/2;同时要注意利用对称性,将所比较的数值对应的自娈量转化到同一个单调区间之上,才能利用函数的单调性得出相应结果。
★题4、已知函数f(x)= x2-2(1-a)x+2,在(-∞,4)上是减函数,求出实数a之取值范围。
 解;见教材全解P109例题5;a≤-3;二次函数的问题要特别注意三点:开口方向,对称轴,顶点坐标。
解;见教材全解P109例题5;a≤-3;二次函数的问题要特别注意三点:开口方向,对称轴,顶点坐标。
★题4、图中的图象所表示的函数的解析式为( B )
A.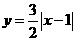
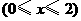
B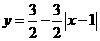
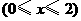
C.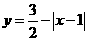
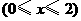
D.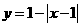
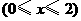
★题6.设函数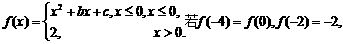 则关于x的方程
则关于x的方程
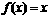 解的个数为 ( C )A.1 B.2 C.3 D.4
解的个数为 ( C )A.1 B.2 C.3 D.4
★题7.若不等式x2+ax+1³0对于一切xÎ(0,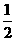 )成立,则a的取值范围是( C )
)成立,则a的取值范围是( C )
A.0 B. –2 C.-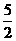 D.-3
D.-3
●解:设f(x)=x2+ax+1,则对称轴为x=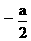 ;若
;若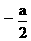 ³
³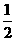 ,即a£-1时,则f(x)在(0,
,即a£-1时,则f(x)在(0,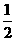 )上是减函数,应有f(
)上是减函数,应有f(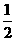 )³0Þ-
)³0Þ-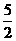 £x£-1若
£x£-1若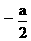 £0,即a³0时,则f(x)在(0,
£0,即a³0时,则f(x)在(0,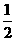 )上是增函数,应有f(0)=1>0恒成立,故a³0若0£
)上是增函数,应有f(0)=1>0恒成立,故a³0若0£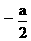 £
£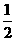 ,即-1£a£0,则应有f(
,即-1£a£0,则应有f(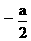 )=
)=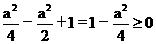 恒成立,故-1£a£0,综上,有-
恒成立,故-1£a£0,综上,有-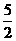 £a故选C
£a故选C
★例题1、设函数f(x)= -ax,其中a≥1,证明:函数f(x)为区间[0,+∞)的↘
●解:注意分子有理化。
★ 例题2、定义于R上的函数y=f(x),有f(0)≠0,,当x>0时f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)·f(b);(1)、证明:f(0)=1;(2)、对任意的x∈R,恒有f(x)>0;(3)、证明:f(x)是R上的增函数;(4)若f(x)·f(2x-x2)>1,求x的取值范围。
●解:①、抽象函数的单调性的证明,注意利用f(x2)=f(x2-x1+x1)或令f(x2)=f(x1+t)(其中t>0)去灵活变形。 ②、注意转化为函数的单调性去处理不等式:x∈(0,3)
●今日作业:
[★题1]已知函数:①、y=x2+2x+5; ②y=-x2-4x+3
(1)、分别写出它们的单调区间;(2)分别求出它们在[0,5)上的值域;
[★题2]设¦(x+1)的定义域为[-2,3)则¦(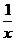 +2)的定义域为___({x|x≤或x>}
+2)的定义域为___({x|x≤或x>}
[★例题3]、将进货单价为80元的商品400个,按90元一个售出时全部卖出,已知这种商品每个涨价1元,其销售个数就减少20个,为了获得最大利润,售价应定为每个多少元。
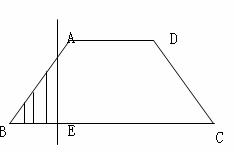 ★[题4]如右图,已知底角45º为的等腰梯形ABCD,底边BC长为7,腰长为
★[题4]如右图,已知底角45º为的等腰梯形ABCD,底边BC长为7,腰长为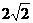 ,当一条垂直于底边BC(垂足为E)的直线
,当一条垂直于底边BC(垂足为E)的直线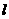 从左至右移动(与梯形ABCD有公共点)时,直线
从左至右移动(与梯形ABCD有公共点)时,直线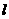 把梯形分成两部分,令BE=x,试写出图中阴影部分的面积y与x的函数关系式.
把梯形分成两部分,令BE=x,试写出图中阴影部分的面积y与x的函数关系式.
解: 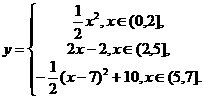
湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义
讲义九: 函数的基本性质----单调性和最值(2)
撰稿: 方锦昌 电子邮箱 fangjingchang2 007@ 手机号码 13975987411
★例题1、证明函数y=x3-b(b为常数)是R上的增函数。(见教案P40面题1)
★例题2、定义(-1,1)上的函数f(x)是↘,且满足f(1-a)<f(a),求实数a的取值范围。
● 解:0<a<1/2. (见教案P40面题2)
★例题3、求函数y= (当-2≤x≤1时),求出其最大值和最小值
●解:最大值为,最小值为0。见教案P44面题补充练习题)
●★例题4、已知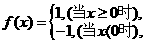 则不等式
则不等式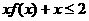 ≤5的解集是
.x≤3/2
≤5的解集是
.x≤3/2
4.课堂作业:书P43 1、2、3题。
3.讨论f(x)=x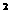 -2x的单调性。 推广:二次函数的单调性
-2x的单调性。 推广:二次函数的单调性
2.判断f(x)=|x|、y=x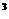 的单调性并证明。
的单调性并证明。
1.求证f(x)=x+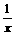 的(0,1]上是减函数,在[1,+∞)上是增函数。
的(0,1]上是减函数,在[1,+∞)上是增函数。
2.教学增函数、减函数的证明:
①出示
★例1:指出函数f(x)=-3x+2、g(x)=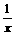 的单调区间及单调性,并给出证明。
的单调区间及单调性,并给出证明。
(由图像指出单调性→示例f(x)=-3x+2的证明格式→练习完成。)
②出示例2:物理学中的玻意耳定律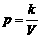 (k为正常数),告诉我们对于一定量的气体,当其体积V增大时,压强p如何变化?试用单调性定义证明.
(k为正常数),告诉我们对于一定量的气体,当其体积V增大时,压强p如何变化?试用单调性定义证明.
(学生口答→ 演练证明)
③小结:比较函数值的大小问题,运用比较法而变成判别代数式的符号。
判断单调性的步骤:设x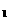 、x
、x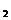 ∈给定区间,且x
∈给定区间,且x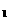 <x
<x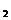 ; →计算f(x
; →计算f(x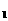 )-f(x
)-f(x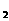 )至最简→判断差的符号→下结论。
)至最简→判断差的符号→下结论。
1.教学增函数、减函数、单调性、单调区间等概念:
①根据f(x)=3x+2、 f(x)=x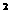 (x>0)的图象进行讨论:
(x>0)的图象进行讨论:
随x的增大,函数值怎样变化? 当x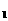 >x
>x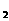 时,f(x
时,f(x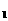 )与f(x
)与f(x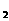 )的大小关系怎样?
)的大小关系怎样?
②.一次函数、二次函数和反比例函数,在什么区间函数有怎样的增大或减小的性质?
③定义增函数:设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说f(x)在区间D上是增函数(increasing function)
④探讨:仿照增函数的定义说出减函数的定义;→ 区间局部性、取值任意性
⑤定义:如果函数f(x)在某个区间D上是增函数或减函数,就说f(x)在这一区间上具有(严格的)单调性,区间D叫f(x)的单调区间。
⑥讨论:图像如何表示单调增、单调减?所有函数是不是都具有单调性?单调性与单调区间有什么关系?y=x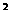 的单调区间怎样?
的单调区间怎样?
③练习(口答):如图,定义在[-4,4]上的f(x),根据图像说出单调区间及单调性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com