(一)、基本概念及知识体系：

教学要求：理解奇函数、偶函数的概念及几何意义，能熟练判别函数的奇偶性。

教学重点：熟练判别函数的奇偶性。

教学难点：理解奇偶性。

教学过程：

[题1]、二次函数¦(x)=ax²+bx (a,b为常数且a≠0)满足¦(-x+5)=¦(x-3)且方程¦(x)=x有等根；①求¦(x)的解析式；②是否存在实数m、n(m <n)使¦(x)定义域为[m，n]，值域为[3m，3n]，若存在，求出m、n之值，若不存在，说明理由

解、①¦(x)=-x²+x　 ②由于¦(x)的值域是¦(x)≤,则3n≤,即n≤,所以有¦(m)=3m且¦(n)=3n　　

∴存在实数m=-4,n=0使¦(x)定义域为[-4，0]，值域为[-12，0]

★例2：某产品单价是120元，可销售80万件。市场调查后发现规律为降价x元后可多销售2x万件，写出销售金额y(万元)与x的函数关系式，并求当降价多少个元时，销售金额最大？最大是多少

分析：此题的数量关系是怎样的？函数呢？如何求函数的最大值？？

小结：利用函数的单调性(主要是二次函数)解决有关最大值和最大值问题。

★题3：①、求函数y＝x+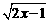的值域。

②、判断函数y=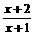单调区间并证明。 (定义法、图象法； 推广： 的单调性)

③、讨论y=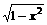在[-1,1]上的单调性。　 (思路：先计算差，再讨论符号情况。)

★　　　 [例题4]某村计划建造一个室内面积为800m²的矩形蔬菜温室，在温室内，沿左、右两侧与后侧内墙各保留1m宽的通道，沿前侧内墙保留3m宽的空地。当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？

★[例题5]、(06·重庆·T₂₁·12分)已知定义域为R的函数f(x)满足¦(f(x)-x²+x)=f(x)-x²+x.

(Ⅰ)若f(2)=3,求f(1);又若f(0)=a,求f(a)；(Ⅱ)设有且仅有一个实数x₀,使得f(x_0­)= x_0,求函数f(x)的解析表达式.

▲解：(Ⅰ)因为对任意x∈R，有f(f(x)- x² + x)=f(x)- x² +x，所以f(f(2)- 2²+2)=f(2)- 2²+2.

又由f(2)=3，得f(3-2²+2)-3-2²+2，即f(1)=1.；若f(0)=a，则f(a-0²+0)=a-0²+0，即f(a)=a.

(Ⅱ)因为对任意xεR，有f(f(x))- x² +x)=f(x)- x² +x.；又因为有且只有一个实数x₀,使得f(x₀)- x_0.

所以对任意x∈R，有f(x)- x² +x= x_0.；在上式中令x= x₀,有f(x₀)-x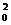 + x₀₌ x_0,

又因为f(x₀)- x₀，所以x_0- x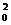=0，故x₀₌0或x₀=1.；若x₀=0，则f(x)- x² +x=0，即f(x)= x² –x.

但方程x² –x=x有两上不同实根，与题设条件矛质，故x₂≠0.

若x₂=1,则有f(x)- x² +x=1，即f(x)= x² –x+1.易验证该函数满足题设条件.

综上，所求函数为f(x)= x² –x+1(x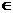R).

★　　　 　

湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义

讲义十：　　 函数的基本性质-----奇偶性 　　　　

撰稿： 方锦昌　 电子邮箱 fangjingchang2 007@　　 手机号码 13975987411

3. 课堂作业：书P43 A组5题；B组1、2题.

2.一个星级旅馆有150个标准房，经过一段时间的经营，经理得到一些定价和住房率的数据如右：

欲使每天的的营业额最高，应如何定价？

　(分析变化规律→建立函数模型→求解最大值)

1. 求下列函数的最大值和最小值：

(1)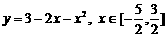；　 (2)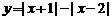

3. 看书P34 例题　 → 口答P36练习　 →小结：最大(小)值定义 ；三种求法.

2.教学例题：

① 出示

★例题1：一枚炮弹发射，炮弹距地面高度h(米)与时间t(秒)的变化规律是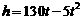，那么什么时刻距离达到最高？射高是多少？

　(学生讨论方法 → 师生共练：配方、分析结果 → 探究：经过多少秒落地？)

② 练习：一段竹篱笆长20米，围成一面靠墙的矩形菜地，如何设计使菜地面积最大？

　 (引导：审题→设变量→建立函数模型→研究函数最大值； →小结：数学建模)

③ 出示

★例2：求函数在区间[3，6]上的最大值和最小值．

　 分析：函数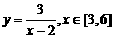的图象 → 方法：单调性求最大值和最小值.

　 → 板演 → 小结步骤：先按定义证明单调性，再应用单调性得到最大(小)值.

　 → 变式练习：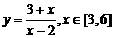

④ 探究：的图象与的关系？

⑤ 练习：求函数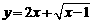的最小值. (解法一：单调法；　 解法二：换元法)

1.教学函数最大(小)值的概念：

① 指出下列函数图象的最高点或最低点，→ 能体现函数值有什么特征？

，　　　 ；，

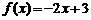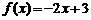
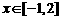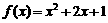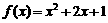
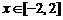
② 定义最大值：设函数y=f(x)的定义域为I，如果存在实数M满足：对于任意的x∈I，都有f(x)≤M；存在x₀∈I，使得f(x₀) = M. 那么，称M是函数y=f(x)的最大值(Maximum Value)

③ 探讨：仿照最大值定义，给出最小值(Minimum Value)的定义．

　 → 一些什么方法可以求最大(小)值？(配方法、图象法、单调法) → 试举例说明方法.

3.知识回顾：增函数、减函数的定义。

2. f(x)＝ax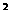+bx+c的最小值的情况是怎样的？