
题目列表(包括答案和解析)
★●例题1、已知函数f(x)= x2+在区间[a,b]上的最小值为2a,最大值为2b,求出适合条件的区间[a,b] ●解:(见教案P56面题1)[1,3]或[-2-,]
★例题2、已知函数f(x)的定义域为R,且对于任意的x和y,都有f(x+y)=f(x)+f(y),又当x>0时,f(x)<0,f(1)=-2,(1)、证明函数f(x)为奇函数,(2)、求函数f(x)在[-3,3]上的最值。
●解:(见教案P56面题2)最大值为6,最小值为-6
★例题3、已知函数f(x)是定义于(0,+∞)上的增函数,且f()=f(x)-f(y),
(1)、求出f(1)之值;(2)、若f(6)=1,解不等式f(x+3)+f()≤2 解:(见教案P63面题2)x≥
●例题:已知集合A={x|x2-3x-10≤0},B={x|m+1≤x≤2m-1},若A∪B=A,求出实数m的取值范围。 解:(见教案P63面题1)m≤3
★例题1、已知定义于区间(-1,1)上的奇函数f(x)是其定义域上的减函数,且满足f(1-m)+f(1-m2)<0,试求m的取值范围。(见教案P50面题1;m∈(0,1))
★例题2、已知函数f(x)对一切的实数x、y都有f(x+y)=f(x)+f(y),(1)、求证:函数f(x)是奇函数;(2)、若已知f(-3)=a,试用a表示出f(24)。((见教案P51面题2;f(24)=-8a)
★[题1]▲①已知函数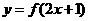 是偶函数,则一定是函数
是偶函数,则一定是函数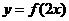 图象的对称轴的直线是(C )A、
图象的对称轴的直线是(C )A、 B、
B、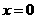 C、
C、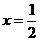 D、
D、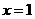
▲②函数y=f(x)与y=g(x)的图象如所示:
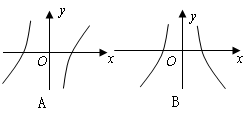 则函数y=f(x)·g(x)的图象可能为( D )
则函数y=f(x)·g(x)的图象可能为( D )

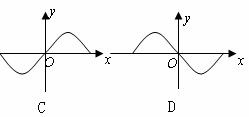
[★题2] 设定义于[-2,2]上的偶函数在区间[0,2]上单调递增,若¦(1-m)<¦(m),求实数m的取值范围(解、<m≤2)
[★题3]①设函数¦(x)是R上的偶函数,且当x∈[0,+∞)时,¦(x)=sinx+x2,求出函数¦(x)的表达式;②已知¦(x)是R上的奇函数,且当x∈(-∞,0)时,有¦(x)=2x+cosx,求出函数¦(x)的表达式
[★题4]已知函数¦(x)的定义域为R,且满足¦(x+2)=-¦(x);
①求证:¦(x)是周期函数;②设¦(x)为奇函数,且0≤x≤1 时¦(x)=x,求 ¦(x)= 的所有x之值 解、周期为4,在一个周期上的根为x=-1,则所有的根为x=4n-1;(n∈z)
[★题5]设a为实数,函数¦(x)= x2+|x-a|+1 ( x∈R)
①讨论函数¦(x)的奇偶性;②求函数¦(x)的最小值
★[题6](2006年辽宁文科T2)设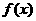 是
是 上的任意函数,下列叙述正确的是( C )
上的任意函数,下列叙述正确的是( C )
A、 是奇函数;
B、
是奇函数;
B、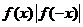 是奇函数;
是奇函数;
C、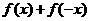 是偶函数;
D、
是偶函数;
D、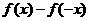 是偶函数
是偶函数
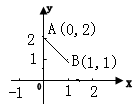 ●解:A中:
●解:A中: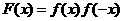 则
则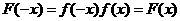 ,即函数
,即函数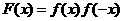 为偶函数;B中:
为偶函数;B中: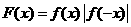 ,
,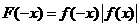 此时
此时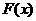 与
与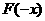 的关系不能确定,即函数
的关系不能确定,即函数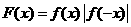 的奇偶性不确定;C中:
的奇偶性不确定;C中: ,
,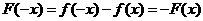 ,即函数
,即函数 为奇函数;D中
为奇函数;D中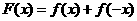 ,
,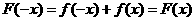 ,即函数
,即函数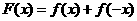 为偶函数,故选择答案C。
为偶函数,故选择答案C。
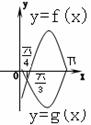 ★[题7]①已知函数y=¦(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象如所示为线段AB,求出它在区间[1,2]上的表达式
★[题7]①已知函数y=¦(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象如所示为线段AB,求出它在区间[1,2]上的表达式
②已知定义于[-π,π]上的函数¦(x)、g(x)分别是偶函数、奇函数,且它们在[0,π]上的图象如图所示,则不等式<0的解集是_____(答案:(-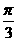 ,0)∪(
,0)∪(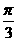 ,π))
,π))
[★题8](2006年重庆文科T21题·12分)已知定义域为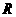 的函数
的函数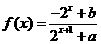 是奇函数。(Ⅰ)求
是奇函数。(Ⅰ)求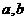 的值;(Ⅱ)若对任意的
的值;(Ⅱ)若对任意的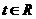 ,不等式
,不等式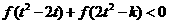 恒成立,求
恒成立,求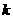 的取值范围;
的取值范围;
解:(Ⅰ)因为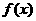 是奇函数,所以
是奇函数,所以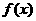 =0,即
=0,即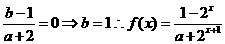 又由f(1)= -f(-1)知
又由f(1)= -f(-1)知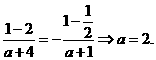 ;(Ⅱ)解法一:由(Ⅰ)知
;(Ⅱ)解法一:由(Ⅰ)知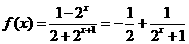 ,易知
,易知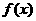 在
在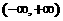 上为减函数。又因
上为减函数。又因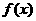 是奇函数,从而不等式:
是奇函数,从而不等式: 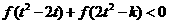 等价于
等价于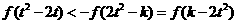 ,因
,因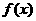 为减函数,由上式推得:
为减函数,由上式推得: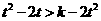 .即对一切
.即对一切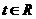 有:
有: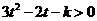 ,分离变量可得k<-
,分离变量可得k<-
4.已知f(x)是奇函数,且在[3,7]是增函数且最大值为4,那么f(x)在[-7,-3]上是( )函数,且最 值是 。
3.已知函数f(x),对任意实数x、y,都有f(x+y)=f(x)+f(y),试判别f(x)的奇偶性。(特值代入)
2.已知f(x)是奇函数,g(x)是偶函数,且f(x)-g(x)=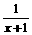 ,求f(x)、g(x)。
,求f(x)、g(x)。
1.设f(x)=ax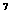 +bx+5,已知f(-7)=-17,求f(7)的值。(答案为27)
+bx+5,已知f(-7)=-17,求f(7)的值。(答案为27)
3.教学奇偶性与单调性综合的问题:
★例3:已知f(x)是奇函数,且在(0,+∞)上是减函数,问f(x)的(-∞,0)上的单调性。
②找一例子说明判别结果(特例法) → 按定义求单调性,注意利用奇偶性和已知单调区间上的单调性。 (小结:设→转化→单调应用→奇偶应用→结论)
③变题:已知f(x)是偶函数,且在[a,b]上是减函数,试判断f(x)在[-b,-a]上的单调性,并给出证明。
2.教学奇偶性判别:
●例1:判别下列函数的奇偶性:
f(x)=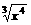 、f(x)=
、f(x)=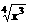 、f(x)=-4x
、f(x)=-4x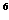 +5x
+5x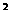 、f(x)=
、f(x)=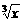 +
+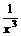 、f(x)=2x
、f(x)=2x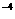 +3。
+3。
★ 判别下列函数的奇偶性:
f(x)=|x+1|+|x-1| f(x)=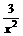 、f(x)=x+
、f(x)=x+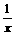 、 f(x)=
、 f(x)=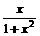 、f(x)=x
、f(x)=x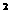 ,x∈[-2,3]
,x∈[-2,3]
③ 小结奇偶性判别方法:先考察定义域是否关于原点对称,再用比较法、计算和差、比商法判别f(x)与f(-x)的关系。 →思考:f(x)=0的奇偶性?
1.教学奇函数、偶函数的概念:
①给出两组图象: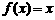 、
、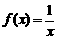 、
、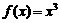 ;
;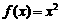 、
、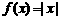 .
.
发现各组图象的共同特征 → 探究函数解析式在函数值方面的特征
② 定义偶函数:一般地,对于函数 定义域内的任意一个x,都有
定义域内的任意一个x,都有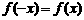 ,那么函数
,那么函数 叫偶函数(even function).
叫偶函数(even function).
③ 探究:仿照偶函数的定义给出奇函数(odd function)的定义.
(如果对于函数定义域内的任意一个x,都有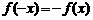 ),那么函数
),那么函数 叫奇函数。
叫奇函数。
④ 讨论:定义域特点?与单调性定义的区别?图象特点?(定义域关于原点对称;整体性)
⑤ 练习:已知f(x)是偶函数,它在y轴左边的图像如图所示,画出它右边的图像。
1.提问:什么叫增函数、减函数?
★2.指出f(x)=2x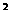 -1的单调区间及单调性。 →变题:|2x
-1的单调区间及单调性。 →变题:|2x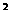 -1|的单调区间
-1|的单调区间
★3.对于f(x)=x、f(x)=x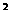 、f(x)=x
、f(x)=x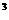 、f(x)=x
、f(x)=x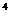 ,分别比较f(x)与f(-x)。
,分别比较f(x)与f(-x)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com