2.基本练习题：

①判别下列函数的奇偶性：(1)、y＝+、　 (2)、y＝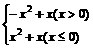

(变式训练：f(x)偶函数，当x>0时，f(x)=….，则x<0时，f(x)=?　 )

①出示

★例1：作出函数y＝x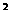－2|x|－3的图像，指出单调区间和单调性。

分析作法：利用偶函数性质，先作y轴右边的，再对称作。→学生作 →口答

→ 思考：y＝|x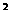－2x－3|的图像的图像如何作？→

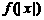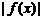②讨论推广：如何由的图象，得到、的图象？

③出示

★例2：已知f(x)是奇函数，在(0，+∞)上是增函数，证明：f(x)在(－∞，0)上也是增函数　　 分析证法 → 教师板演 → 变式训练

④讨论推广：奇函数或偶函数的单调区间及单调性有何关系？

(偶函数在关于原点对称的区间上单调性相反；奇函数在关于原点对称的区间上单调性一致)

2. 教学函数性质的应用：

①出示例3 ：求函数f(x)＝x+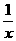 (x>0)的值域。

分析：单调性怎样？值域呢？→小结：应用单调性求值域。 → 探究：计算机作图与结论推广

②出示

2.提问：如何从解析式得到奇函数、偶函数、增函数、减函数、最大值、最小值的定义？

1.讨论：如何从图象特征上得到奇函数、偶函数、增函数、减函数、最大值、最小值？

(二)、教学过程：

(一)、基本概念及知识体系：

教学要求：掌握函数的基本性质(单调性、最大值或最小值、奇偶性)，能应用函数的基本性质解决一些问题。

教学重点：掌握函数的基本性质。　　 教学难点：应用性质解决问题。

湖南省省级示范性高中……洞口三中高一数学第一学期授课讲义

　　　　　　　 讲义十一：函数的基本性质的复习归纳与应用　　　

撰稿： 方锦昌　 电子邮箱 fangjingchang2 007@　　 手机号码 13975987411

3、　 函数的奇偶性的判断方法：①定义法，②图象法。

2、　 图象性质：奇函数的图象关于原点成中心对称；(注意：若¦(0)存在，则必有¦(0)=0Þ处理填空或选择题的法宝)；偶函数的图象关于y轴成轴对称图形。(图象法)

1、　 奇函数、偶函数：¦(x)为奇函数⇔¦(-x)= -¦(x)；¦(x)为偶函数⇔¦(-x)= ¦(x)　 (定义法)