
题目列表(包括答案和解析)
3.要从已编号( )的
)的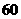 枚最新研制的某型导弹中随机抽取
枚最新研制的某型导弹中随机抽取 枚来进行发射试验,用每部分
枚来进行发射试验,用每部分
选取的号码间隔一样的系统抽样方法确定所选取的 枚导弹的编号可能是( )
枚导弹的编号可能是( )
A. B.
B. C.
C. D.
D.
2.某同学使用计算器求 个数据的平均数时,错将其中一个数据
个数据的平均数时,错将其中一个数据 输入为
输入为 ,那么由此求出的
,那么由此求出的
平均数与实际平均数的差是( ) A.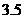 B.
B. C.
C.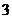 D.
D.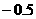
1. 名工人某天生产同一零件,生产的件数是
名工人某天生产同一零件,生产的件数是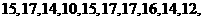 设其平均数为
设其平均数为 ,
,
中位数为 ,众数为
,众数为 ,则有( )
,则有( )
A.  B.
B. C.
C. D.
D.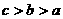
(五)、2007年高考试题摘录:
★题1、(07天津)在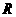 上定义的函数
上定义的函数 是偶函数,且
是偶函数,且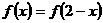 ,若
,若 在区间
在区间 是减函数,则函数
是减函数,则函数 ( B )A.在区间
( B )A.在区间 上是增函数,区间
上是增函数,区间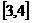 上是增函数;B.在区间
上是增函数;B.在区间 上是增函数,区间
上是增函数,区间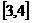 上是减函数;C.在区间
上是减函数;C.在区间 上是减函数,区间
上是减函数,区间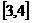 上是增函数;D.在区间
上是增函数;D.在区间 上是减函数,区间
上是减函数,区间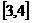 上是减函数
上是减函数
★题2、(07浙江)设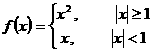 ,
, 是二次函数,若
是二次函数,若 的值域是
的值域是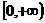 ,则
,则 的值域是( C )A.
的值域是( C )A. B.
B. C.
C.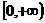 D.
D. 
★题3、 (07福建)已知函数 为R上的减函数,则满足
为R上的减函数,则满足 的实数
的实数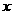 的取值范围是(C )A.
的取值范围是(C )A. B.
B.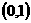 C.
C. D.
D.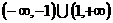
★题4、 (07福建)已知函数 为R上的减函数,则满足
为R上的减函数,则满足 的实数
的实数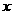 的取值范围是(C )A.
的取值范围是(C )A. B.
B.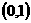 C.
C. D.
D.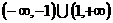
★题5、(07重庆)已知定义域为R的函数 在区间
在区间 上为减函数,且函数
上为减函数,且函数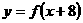 为偶函数,则( D )A.
为偶函数,则( D )A. B.
B. 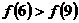 C.
C. 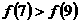 D.
D. 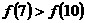
★题6、(07安徽)若对任意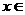 R,不等式
R,不等式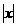 ≥ax恒成立,则实数a的取值范围是(B)
≥ax恒成立,则实数a的取值范围是(B)
A. a<-1
B.  ≤1
C.
≤1
C. <1
D.a≥1
<1
D.a≥1
★题7、(07安徽)定义在R上的函数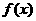 既是奇函数,又是周期函数,
既是奇函数,又是周期函数, 是它的一个正周期.若将方程
是它的一个正周期.若将方程 在闭区间
在闭区间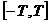 上的根的个数记为
上的根的个数记为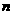 ,则
,则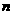 可能为(D)
可能为(D)
A.0 B.1 C.3 D.5
★题8、(07安徽)图中的图象所表示的函数的解析式为(B)
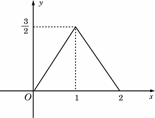 (A)
(A) (0≤x≤2)
(0≤x≤2)
(B) 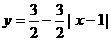 (0≤x≤2)
(0≤x≤2)
(C)  (0≤x≤2)
(0≤x≤2)
(D)
 (0≤x≤2)
(0≤x≤2)
★题9、 (07重庆)若函数 的定义域为R,则实数
的定义域为R,则实数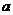 的取值范围 。
的取值范围 。 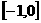
★题10、(07宁夏)设函数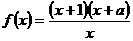 为奇函数,则实数
为奇函数,则实数 。-1
。-1
★题11、(07上海)已知函数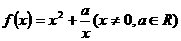 ;(1)判断函数
;(1)判断函数 的奇偶性;
的奇偶性;
(2)若 在区间
在区间 是增函数,求实数
是增函数,求实数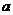 的取值范围。
的取值范围。
解:(1)当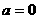 时,
时, 为偶函数;当
为偶函数;当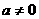 时,
时, 既不是奇函数也不是偶函数.
既不是奇函数也不是偶函数.
(2)设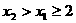 ,
,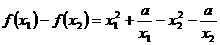
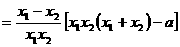 ,
,
由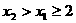 得
得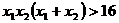 ,
, ;要使
;要使 在区间
在区间 是增函数只需
是增函数只需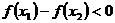 ,即
,即 恒成立,则
恒成立,则 。
。
★例题1、画出下列分段函数f(x)=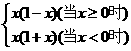 的图象:(见教案P35面例题2)
的图象:(见教案P35面例题2)
★例题2、已知函数f(x)= ,确定函数的定义域和值域;判断函数的奇偶性、单调性。(见教案P35面例题3)
,确定函数的定义域和值域;判断函数的奇偶性、单调性。(见教案P35面例题3)
★[例题3]某地区上年度电价为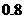 元/kW
元/kW ,年用电量为
,年用电量为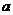 kW
kW 。本年度计划将电价降到
。本年度计划将电价降到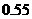 元/kW
元/kW 至
至 元/kW
元/kW 之间,而用户期望电价为
之间,而用户期望电价为 元/kW
元/kW 经测算,下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为K)。该地区电力的成本为
经测算,下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为K)。该地区电力的成本为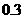 元/kW
元/kW 。
。
(I)写出本年度电价下调后,电力部门的收益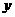 与实际电价
与实际电价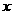 的函数关系式;
的函数关系式;
(II)设 ,当电价最低定为多少时仍可保证电力部门的收益比上年至少增长20%?
,当电价最低定为多少时仍可保证电力部门的收益比上年至少增长20%?
(注:收益=实际用电量×(实际电价-成本价))
解:(I):设下调后的电价为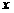 元/
元/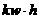 ,依题意知用电量增至
,依题意知用电量增至 ,电力部门的收益为
,电力部门的收益为
 (II)依题意有
(II)依题意有
 整理得
整理得 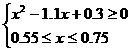
解此不等式得 
答:当电价最低定为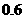
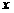 元/
元/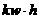 仍可保证电力部门的收益比上年至少增长20%。
仍可保证电力部门的收益比上年至少增长20%。
★[例题5]某地为促进淡水鱼养殖业的发展,将价格控制在适当范围内,决定对淡水鱼养值提供政府补贴.设淡水鱼的市场价格为x元/千克,政府补贴为t元/千克.根据市场调查,当8≤x≤14时,淡水鱼的市场日供应量P千克与市场日需求量Q千克近似地满足关系: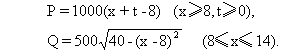 当P=Q时市场价格称为市场平衡价格.
当P=Q时市场价格称为市场平衡价格.
(1)将市场平衡价格表示为政府补贴的函数,并求出函数的定义域;
(2)为使市场平衡价格不高于每千克10元,政府补贴至少为每千克多少元?
●解:(1)依题设有 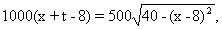 化简得
5x2+(8t-80)x+(4t2-64t+280)=0.当判别式△=800-16t2≥0时,
化简得
5x2+(8t-80)x+(4t2-64t+280)=0.当判别式△=800-16t2≥0时,
 由△≥0,t≥0,8≤x≤14,得不等式组:
由△≥0,t≥0,8≤x≤14,得不等式组: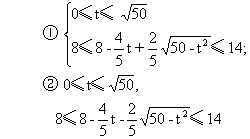 解不等式组①,得
解不等式组①,得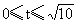 ,不等式组②无解.故所求的函数关系式为
,不等式组②无解.故所求的函数关系式为 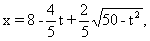

(2)为使x≤10,应有
 化简得t2+4t-5≥0.解得t≥1或t≤-5,由t≥0知t≥1.从而政府补贴至少为每千克1元.
化简得t2+4t-5≥0.解得t≥1或t≤-5,由t≥0知t≥1.从而政府补贴至少为每千克1元.
5. 课堂作业: P43 A组6题, B组2、3题。
4. 求二次函数f(x)=x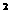 -2ax+2在[2,4]上的最大值与最小值。
-2ax+2在[2,4]上的最大值与最小值。
3. f(x)是定义在(-1,1)上的减函数,如何f(2-a)-f(a-3)<0。求a的范围。
2.已知函数f(x)=ax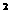 +bx+3a+b为偶函数,其定义域为[a-1,2a],求函数值域。
+bx+3a+b为偶函数,其定义域为[a-1,2a],求函数值域。
1.求函数y= 为奇函数的时,a、b、c所满足的条件。
(c=0)
为奇函数的时,a、b、c所满足的条件。
(c=0)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com