
题目列表(包括答案和解析)
6.设集合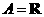 ,集合
,集合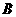 =正实数集,则从集合
=正实数集,则从集合 到集合
到集合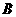 的映射只可能是( C )
的映射只可能是( C )
A.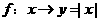 B.
B.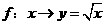
C.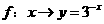 D.
D.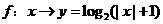
5.下列各组函数中,表示同一个函数的是:( D )
A、y=x-1和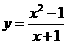 B、y=x0和y=1
B、y=x0和y=1
C、f(x)=x2 和g(x)=(x+1)2
D、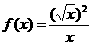 和
和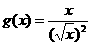
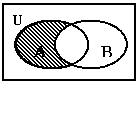
4.右图中阴影部分所对应的集合是( C )
A. (CUA)ÇB B. CU(AÈB) C. (CUB)ÇA D. CU(AÇB)
3. 已知集合A={1,a2},实数a不能取的值的集合是(A )
已知集合A={1,a2},实数a不能取的值的集合是(A )
A.{-1,1} B.{-1} C.{-1,0,1} D.{1}
2.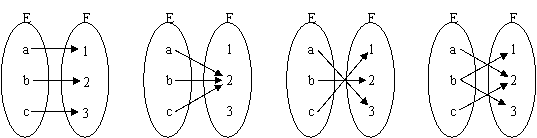 在下列集合E到集合F的对应中,不能构成E到F的映射是( D )
在下列集合E到集合F的对应中,不能构成E到F的映射是( D )
A B C D
1.设集合P={3,4,5},Q={4,5,6,7},定义P·Q={(a,b) |a∈P,b∈Q},则P·Q中元素的个数为( )D
A. 3 B. 7 C.10 D.12
21.解:(1)令t=+.
要使有t意义,必须1+x≥0且1-x≥0,即-1≤x≤1,
∴t2=2+2.∴t2∈[2,4]且t≥0 .t的取值范围是[,2].
(2)∵t2=2+2,∴=t2-1.∴m(t)=a(t2-1)+t=at2+t-a,t∈[,2].
(3) h(t)=a(t2-1)+t=at2+t-a,t∈[,2].
∵a<0,∴函数y=h(t), t∈ [,2]的图象是开口向下的抛物线的一段.
h(t)=at2+t-a=a(t+)2-a-.
若-∈[0,]时,即a≤-,则g(a)=h()=;
若-∈(,2]时,即-<a≤-,则g(a)=h(-)=-a-;
若-∈(2,+∞)时,即-<a<0,则g(a)=h(2)=a+2.
综上有g(a)=
20.解:(1)如右图所示.
(2)方程f(x)=5的解分别是2-,0,4和2+,
由于f(x)在(-∞,-1]和[2,5]上单调递减,
在[-1,2]和[5,+∞)上单调递增,
因此A=(-∞,2-]∪[0,4]∪[2+ ,+∞).
由所以B⊆A.
19.解:(1)A={0,-4}.又因为A∪B=B,所以AÍB.
又B为一元二次方程的解集,最多有两个元素,因此B=A={0,-4}.
即 解得a=1.
所以若A∪B=B时,实数a的取值范围是{a| a=1}.
(2)A∩B=B即BÍA,则B可能为Æ,{0},{-4},{0,-4}.
当B=Æ时,由△=[2(a+1)]2-4(a2-1)<0,解得a<-1;
当B={0}时,则解得a=-1;
当B={-4}时,则无解;
当B={0,-4}时,由(1)得a=1.
 综上,A∩B=B时,实数a的取值范围是{a| a≤-1或a=1}.
综上,A∩B=B时,实数a的取值范围是{a| a≤-1或a=1}.
18.解:(1)函数f(x)=x(1-)=x(),所以f(-x)=(-x)()=x(),所以
f(x)是偶函数.
(2)当x>0时,2x>1,所以f(x)=x()>0,又因为f(x)是偶函数,所以当x<0时,f(x)=f(-x)>0,于是,当x≠0时,f(x)>0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com