15. 解: (1)　 (4分)

(2) 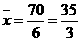, , 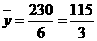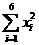=1+16+100+169+324+676=1286.

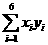=－20+96++26×64=3474　 (8分)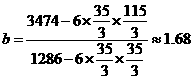　 　

a≈18.73　 (12分)

14. 解: (1) 0.7　 (6分)　　　　 (2) 0.30　 (12分)

13.解: (1) 12÷15%=80 (件)　 (4分)

　　 (2) 第四组: 30%÷15%×12=24 (件)　 (8分)

　　 (3)第四组作品数为24件, 获奖率为10÷24≈41.7%.

　　　 第六组作品数为80×(1－20%-30%-20%-15%-10%)=4(件) 获奖率为2÷4=50%, 所以,第六组获奖率较高. (12分)

9. 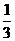　　　10. 60　　　 11.　 499　　　 12.　 120

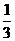18. 甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为和, 求:

(1)甲、乙两人至少有一个人破译出密码的概率;

(2)两人都没有破译出密码的概率.

陕西普通高中新课程教学质量检测学段考试

数学试题(必修模块三　 适用北师大版教材)

17.某商场为了促销,采用购物打折的优惠办法: 每位顾客一次购物:

①在1000元及以上且2000元以下者按九五折优惠;

②在2000元以上且3000元以下者按九折优惠;

③在3000元以上且5000元以下者按八五折优惠;

④在5000元及以上者按八折优惠.

(1)写出函数关系式;

(2)试编写流程图求优惠价.

16.(12分)我国古算术中有一个鸡兔同笼问题, 请完成下列一个算法:

(1)输入鸡和兔的总数量M;

(2)输入鸡和兔的总数量N;

(3)鸡的数量A= 　　　　　　　;

(4)兔的数量B=　　　　　　　 　;

写出程序框图.

第Ⅱ卷　 (附加题　　 满分20分)

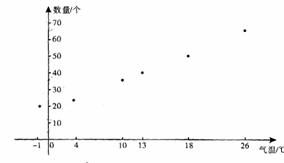
15.(12分)下表是某小卖部6天卖出可乐的数量与当天平均气温的对比表:

(1)将上表中的数据制成散点图;

(2)求线性回归方程系数a、b.

14.(12分)口袋里有若干红球、黄球与蓝球, 随机从中摸一个球,摸到红球的概率为0.40, 摸到黄球的概率为0.30, 求:

(1)摸出的一个为红球或黄球的概率;

(2)摸出的一个为蓝球的概率.

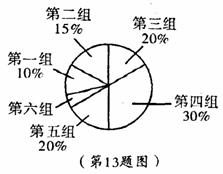
13.(12分)在学校开展的综合实践活动中,某班全班同学分成6个小组, 各小组上交作品如图所示,其中第二组上交了12件.

(1)本次活动共有多少作品参加评比?

(2)哪一组上交的作品数最多?有多少件?

(3)经评比,第四组和第六组分别有10件、2件作品获奖,则这两组中哪一组获奖率较高?