
题目列表(包括答案和解析)
20. (本小题满分14分)若对于正整数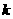 、
、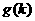 表示
表示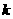 的最大奇数因数,(例如:3的正奇数因数有1、3,所以
的最大奇数因数,(例如:3的正奇数因数有1、3,所以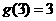 ,又如:20的正奇数因数有1、5,所以
,又如:20的正奇数因数有1、5,所以 ,)并且
,)并且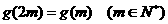 ,设
,设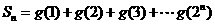
(Ⅰ)求S1、S2、S3 ;(注: 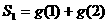 )
)
(Ⅱ)求证: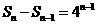 ;
;
(III)设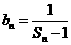 ,求证数列
,求证数列 的前
的前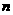 顶和
顶和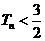 .
.
解:(Ⅰ)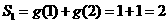 ……1分
……1分
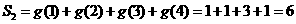 ……2分
……2分
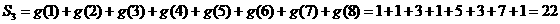 ……3分
……3分
(Ⅱ) ,
,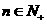 ……4分
……4分

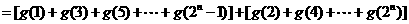
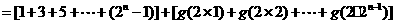 ……5分
……5分
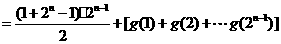 ……6分
……6分
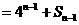
则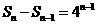 ……7分
……7分
(Ⅲ)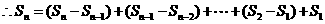 ……8分
……8分
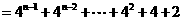
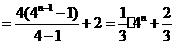 ……9分
……9分
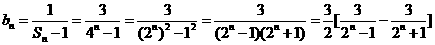 ……10分
……10分
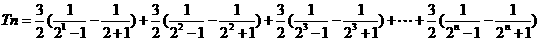
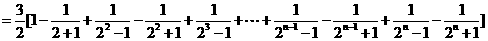
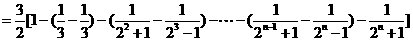 ……11分
……11分
 当
当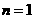 时,
时,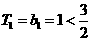 成立 ……12分
成立 ……12分
当 时,
时,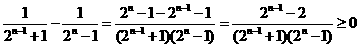 ……13分
……13分

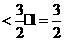 ……14分
……14分

 高一数学第二学期期中考试题
高一数学第二学期期中考试题
19. (本小题满分14分)已知函数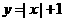 ,
,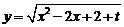 ,
,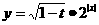 的最小值恰好是方程
的最小值恰好是方程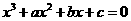 的三个根,其中
的三个根,其中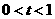 .
.
(Ⅰ)求以上三个函数的最小值;
(Ⅱ)求证: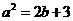 ;
;
(Ⅲ)设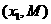 ,
,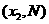 是函数
是函数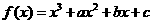 的两个极值点.
的两个极值点.
若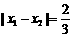 ,求函数
,求函数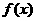 的解析式;
的解析式;
解:(Ⅰ)三个函数的最小值依次为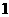 ,
,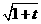 ,
,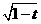 ,…………………… …3分
,…………………… …3分
(Ⅱ)由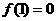 ,得
,得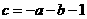 …………………… …4分
…………………… …4分
∴ 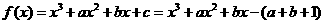
 ,…………………… …5分
,…………………… …5分
故方程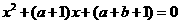 的两根是
的两根是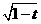 ,
,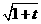 .
.
故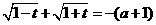 ,
, .………………………7分
.………………………7分
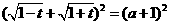 ,即
,即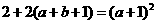
∴ 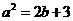 . …………………………………………………………………8分
. …………………………………………………………………8分
(Ⅲ)依题意 是方程
是方程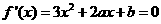 的根,
的根,
故有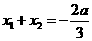 ,
,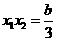 ,…………9分
,…………9分
且△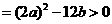 ,得
,得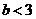 .…………10分
.…………10分
由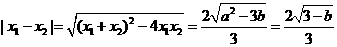
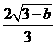
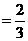 ;得,
;得,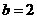 ,
,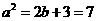 .……………………11分
.……………………11分
由(Ⅰ)知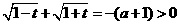 ,故
,故 ,………………12分
,………………12分
∴ 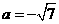 ,
,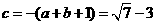 ………………13分
………………13分
∴ 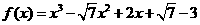 .………………………………………………14分
.………………………………………………14分
18. (本小题满分14分) 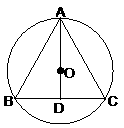 2.如图:在半径为2
2.如图:在半径为2 的圆内,作内接等腰三角形ABC,当底边上高为多少时三角形ABC的面积最大
的圆内,作内接等腰三角形ABC,当底边上高为多少时三角形ABC的面积最大 ?并求出此时三角形的面积。
?并求出此时三角形的面积。
解 设圆内接等腰三角形的底边长为2x,高为h,
设圆内接等腰三角形的底边长为2x,高为h,
那么h=AO+BO=2+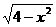 ,解得
,解得
x2=h(4-h),于是内接三角形的面积为
S=x·h=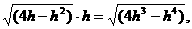
从而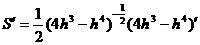

令S′=0,解得h=3,由于不考虑不存在的情况,所在区间(0,4)上列表如下
|
h |
(0,2) |
2 |
(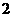 ,4) ,4) |
|
S′ |
+ |
0 |
- |
|
S |
增函数 |
最大值 |
减函数 |
由此表可知,当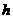 =3时,等腰三角形面积最大
=3时,等腰三角形面积最大 此时
此时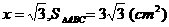
答 当底边上高为3
当底边上高为3 时,等腰三角形面积最大
时,等腰三角形面积最大 ,此时三角形的面积为
,此时三角形的面积为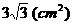 。
。
17. (本小题满分14分)已知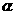 为锐角,且
为锐角,且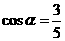 .
.
(Ⅰ)求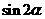 的值;
的值;
(Ⅱ)若cos (2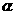 -
-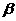 )=-
)=-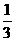 ,
,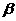 为锐角,求cos
为锐角,求cos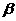 的值.(注:原试卷中”sin (2
的值.(注:原试卷中”sin (2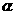 -
-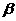 )=-
)=-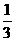 ”,改为”cos (2
”,改为”cos (2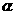 -
-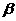 )=-
)=-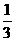 ”)
”)
解:(Ⅰ)由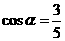 ,
,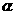 为锐角 得
为锐角 得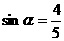 且
且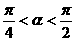 ………2分
………2分
∴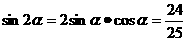 且
且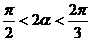 ………4分
………4分
(Ⅱ)由(Ⅰ)得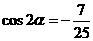 ,
,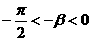 ………6分
………6分
又cos
(2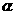 -
-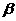 )=-
)=-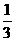 可知
可知 ………8分
………8分
∴sin (2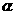 -
-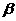 )=
)=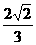 ………10分
………10分
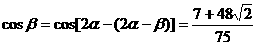 ………14分
………14分
16.(本小题满分12分)设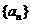 是公比大于1的等比数列,
是公比大于1的等比数列,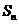 为数列
为数列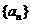 的前
的前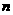 项和.已知
项和.已知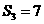 ,且
,且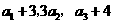 构成等差数列.
构成等差数列.
求数列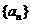 的通项公式和
的通项公式和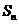
解: 由已知得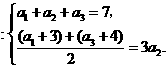 ………2分
………2分
解得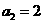 .………4分
.………4分
设数列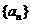 的公比为
的公比为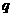 ,由
,由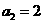 ,可得
,可得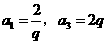 .………6分
.………6分
又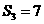 ,可知
,可知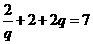 ,
,
即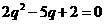 , ………8分
, ………8分
解得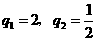 . ………9分
. ………9分
由题意得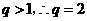 .
.
 .
………10分
.
………10分
故数列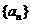 的通项为
的通项为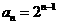 .
.  ………12分
………12分
15.(本小题满分12分)已知tan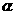 =2, 求
=2, 求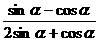 的值;
的值;
解: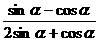 =
=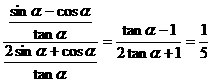 ………12分
………12分
14.设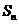 是等比数列
是等比数列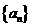 的前
的前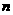 项和, 对于等比数列
项和, 对于等比数列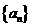 ,有命题
,有命题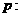 若
若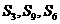 成等差数列,则
成等差数列,则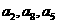 成等差数列成立;对于命题
成等差数列成立;对于命题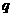 :若
:若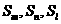 成等差数列, 则
________________成等差数列.请将命题
成等差数列, 则
________________成等差数列.请将命题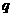 补充完整,使它也是真命题.(只要一个符合要求的答案即可)
补充完整,使它也是真命题.(只要一个符合要求的答案即可)
 开放题,答案不唯一.
开放题,答案不唯一.
13.如右图:直角三角形ABC中,∠B是直角,AD是∠BAC
的平分线,又AD=5,AB=4,求sin∠BAC= .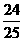
12.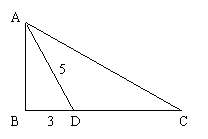 已知角
已知角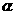 的终边经过点P(-8m, -3 ),且cos
的终边经过点P(-8m, -3 ),且cos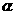 = -
= - ,则m=
.
,则m=
.
11. 在等差数列{ n}中, 已知
n}中, 已知 3+
3+ 11=40, 则
11=40, 则 6+
6+ 7+
7+ 8=__________.60
8=__________.60
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com