
题目列表(包括答案和解析)
8.函数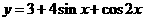 的最大值是(
)
的最大值是(
)
A.0 B.3 C.6 D.8
7.甲乙两人下棋,甲获胜的概率为30%,甲不输的概率为70%,则甲乙两人下一盘棋,最可能出现的情况是( )
A.甲获胜 B.乙获胜 C.二人和棋 D.无法判断
6.函数 的图像的一条对称轴方程是( )
的图像的一条对称轴方程是( )
A.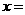
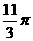 B.
B.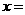
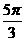 C.
C.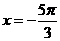 D.
D.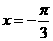
4. (山东5题)(5)已知cos(α-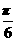 )+sinα=
)+sinα=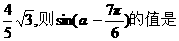 ( )
( )
(A)- (B)
(B) ( C ) -
( C ) - (D)
(D) 
5(广东理5题).在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F,若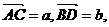 则
则 :
:
A.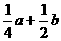 B.
B.
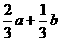 C.
C.
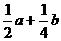 D.
D.
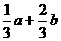
3、(08广东文科5题)已知函数f(x)=(1+cos2x)sin3x,x∈R,则f(x)是( )
A.最小正周期为 的奇函数 B.最小正周期为
的奇函数 B.最小正周期为 的偶函数
的偶函数
C.最小正周期为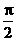 的奇函数 D.最小正周期为
的奇函数 D.最小正周期为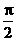 的偶函数
的偶函数
2.(08广东文科3题)已知平面向量=(1,2),=(-2,m),且∥,则2+3= ( )
A.(-2,-4) B.(-3,-6) C.(-4,-8) D.(-5,-10)
1.1920°转化为孤度数为( )
A.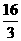 B.
B. C.
C.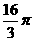 D.
D.
16题、在 中,
中,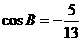 ,
, . (Ⅰ)求
. (Ⅰ)求 的值;(Ⅱ)设
的值;(Ⅱ)设 的面积
的面积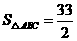 ,求
,求 的长.
的长.
 17题、已知
17题、已知 =(6,1),
=(6,1), =(-2,-3),设
=(-2,-3),设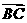 =(x, y)(Ⅰ)若四边形ABCD为梯形,求x、y间的函数的关系式;(Ⅱ)若以上梯形的对角线互相垂直,求
=(x, y)(Ⅰ)若四边形ABCD为梯形,求x、y间的函数的关系式;(Ⅱ)若以上梯形的对角线互相垂直,求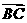 。
。
18题.某地区100位居民的人均月用水量(单位:t)的分组及各组的频数如下: [0,0.5],4;[0.5,1],8;[1,1.5],15;[1.5,2],22;[2,2.5],25;[2.5,3],14;[3,3.5],6;[3.5,4],4;[4,4,5],2。 (Ⅰ)列出样本的频率分布表; (Ⅱ)画出频率分布直方图,并根据直方图估计这组数据的众数; (Ⅲ)当地政府制定了人均月用水量为3t的标准,若超出标准加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗?为什么?
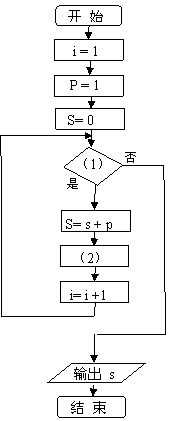
19题、 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先将所给出的程序框图补充完整,再请你根据程序框图写出相应的程序.
20题、已知函数f(x)=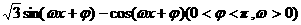 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为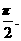 (Ⅰ) 求f(
(Ⅰ) 求f(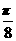 )的值;(Ⅱ)将函数y=f(x)的图象向右平移
)的值;(Ⅱ)将函数y=f(x)的图象向右平移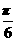 个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
21题.假设你家订了一份报纸,送报人可能在早上6点-8点之间把报纸送到你家,你每天离家去工作的时间在早上7点-9点之间。 (1)你离家前不能看到报纸(称事件A)的概率是多少? (2)请你设计一种随机模拟的方法近似计算事件A的概率(包括手工的方法或用计算器、计算机的方法)
15、从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如表中所示。
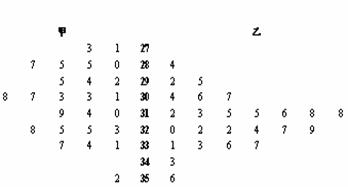 由以上数据设计了如下茎叶图: 根据该茎叶图,对甲乙两品种棉花的纤维长度作比较,请你写出两个统计结论:________
由以上数据设计了如下茎叶图: 根据该茎叶图,对甲乙两品种棉花的纤维长度作比较,请你写出两个统计结论:________
14、 直角坐标平面上三点
直角坐标平面上三点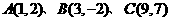 ,若
,若 为线段
为线段 的三等分点,则
的三等分点,则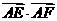 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com