
题目列表(包括答案和解析)
6.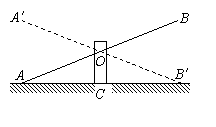 如图是跷跷板的示意图,支柱OC与地面垂直,
如图是跷跷板的示意图,支柱OC与地面垂直,
点O是横板AB的中点,AB可以绕着点O上下转动,
当A端落地时,∠OAC=20°,则横板AB上下可转动
的最大角度(即∠A′OA)是 度 。
5.计算 =
。
=
。
4.如图正方形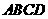 的边长为4cm,则图中阴影部分
的边长为4cm,则图中阴影部分
的面积为 cm2.
3.如图在Rt△ABC中,∠C=90°∠B=30°,AB=2,
 则AC= 。
则AC= 。
2.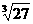 = 。
= 。
1. 在实数
在实数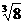 ,
,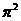 ,
, 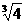 ,
,
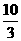 ,
, 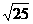 中是
无理数 。
中是
无理数 。
●11.已知集合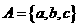 ,写出集合A的所有真子集
,写出集合A的所有真子集
●12. (07重庆卷)已知集合U={1,2,3,4,5,6,7}, A={2,4,5,7},B={3,4,5},则( uA)∪(
uA)∪( uB)=____
uB)=____
●13. (07上海卷)已知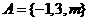 ,集合
,集合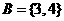 ,若
,若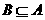 ,则实数
,则实数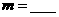 。
。
●14、(07全国卷I)设集合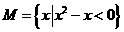 ,
,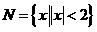 ,则M∩N= _____
,则M∩N= _____
●15、已知集合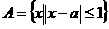 ,
,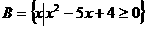 ,若A∩B=Æ,则实数
,若A∩B=Æ,则实数 的取值范围是
的取值范围是
.三、解答题(12+12+12+12+13+14,共75分)
★16(12分)、设U={x∈Z|0<x≤10},A={1,2,4,5,9},B={4,6,7,8,10},C={3,5,7},求
A∩B,A∪B,(CUA)∩(CUB),(CUA)∪(CUB),(A∩B)∩C,(A∪B)∩C。
解:①、A∩B=
②、A∪B=
③、(CUA)∩(CUB)=
④、(CUA)∪(CUB)=
⑤、(A∩B)∩C=
⑥、(A∪B)∩C=
★17(12分)、已知集合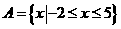 ,
,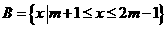 .
.
(1)当m=3时,求集合A∩B; (2)若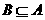 ,求实数m的取值范围.
,求实数m的取值范围.
★18(12分)、已知集合A={x|x2-2x-8=0},B={x|x2+ax+a2-12=0}且有A∪B=A ,求实数a的取值集合。
★19(12分)、已知不等式 对于所有的
对于所有的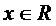 恒成立,求实数
恒成立,求实数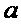 的取值范围
的取值范围
★20(13分)、已知集合A={(x,y)|x2+mx-y+2=0},B={(x,y)|x-y+1=0,0≤x≤2},如果A∩B≠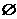 ,求实数m的取值范围.
,求实数m的取值范围.
★ 21题(14分)、若B={x|x2-3x+2<0},请问是否存在实数a,使A={x|x2-(a+a2)x+a3<0}满足:A∩B=A?若存在,请求出a相应的取值范围;若不存在,请说明你的理由.
★1.已知全集 ,
,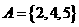 ,则
,则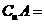 ( )
( )
A. 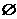 B.
B.
 C.
C.
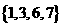 D.
D.
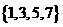
★2.已知集合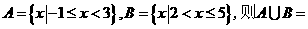 ( )
( )
. A. {x|2<x<3} B. {x|-1≤x≤5} C. {x| -1<x<5} D.{x| -1<x≤5}
★
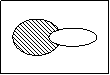 3.图中阴影部分表示的集合是( )
3.图中阴影部分表示的集合是( )
 A. A∩CUB B.CUA∩B
A. A∩CUB B.CUA∩B
C.CU(A∩B) D. CU(A∪B)
★4.方程组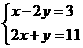 的解集是( )
的解集是( )
A . 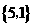 B.
B.
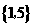 C.
C.
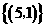 D.
D.

★5.已知集合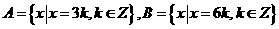 , 则A与B之间最适合的关系是( )
, 则A与B之间最适合的关系是( )
A.、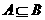 B.、
B.、 C、AÜB.
D.、AÝB
C、AÜB.
D.、AÝB
★6.(07江西)若集合M={0,l,2},N={(x,y)|x-2y+1≥0且x-2y-1≤0,x,y ∈M},则N中元素的个数为( )
A.9 B.6 C.4 D.2 C.
★7.(07湖北)集合P={x」x2-16<0},Q={x」x=2n,n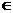 Z},则P∩Q=( )
Z},则P∩Q=( )
A.{-2,2} B.{-2,2,-4,4} C.{-2,0,2} D.{-2,2,0,-4,4}
★8.(07江西卷)已知集合M={x|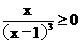 },N={y|y=3x2+1,xÎR},则MÇN=(
)
},N={y|y=3x2+1,xÎR},则MÇN=(
)
A.Æ B. {x|x³1} C.{x|x>1} D. {x| x³1或x<0}
★9、(07辽宁卷)设集合 ,则满足
,则满足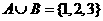 的集合B的个数是( )
的集合B的个数是( )
(A)1 (B)3 (C)4 (D)8
★10、(06湖北卷)有限集合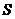 中元素的个数记做
中元素的个数记做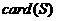 ,设
,设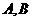 都为有限集合,给出下列命题:
都为有限集合,给出下列命题:
① 的充要条件是
的充要条件是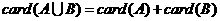 ;②
;②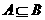 的必要条件是
的必要条件是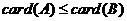 ;③A
;③A B的充分条件是
B的充分条件是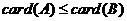 ;④
;④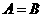 的充要条件是
的充要条件是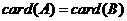 ;其中真命题的序号是( ):A.③④
B.①② C.①④ D.②③
;其中真命题的序号是( ):A.③④
B.①② C.①④ D.②③
选择题答案:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
★16、设U={x∈Z|0<x≤10},A={1,2,4,5,9},B={4,6,7,8,10},C={3,5,7},求
A∩B,A∪B,(CUA)∩(CUB),(CUA)∪(CUB),(A∩B)∩C,(A∪B)∩C。
★17、已知R为全集,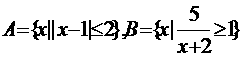 , 求
, 求 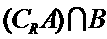 。
。
★18、不等式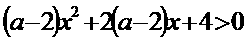 对于
对于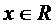 恒成立,求
恒成立,求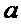 的取值范围
的取值范围
★19、已知M={x|
-2≤x≤5},
N={x| a+1≤x≤2a-1};(Ⅰ)若M N,求实数a的取值范围;(Ⅱ)若M
N,求实数a的取值范围;(Ⅱ)若M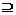 N,求实数a的取值范围.
N,求实数a的取值范围.
解:(Ⅰ)由于M N,则
N,则 ,解得a∈Φ.(Ⅱ)①当N=Φ时,即a+1>2a-1,有a<2;
,解得a∈Φ.(Ⅱ)①当N=Φ时,即a+1>2a-1,有a<2;
②当N≠Φ,则 ,解得2≤a≤3,综合①②得a的取值范围为a≤3.
,解得2≤a≤3,综合①②得a的取值范围为a≤3.
★20、已知集合A={x|x2-5x+4≤0} B={x|x2-2ax+a+2≤0}若A∪B=A求a的取值范围
解、A={x|1≤x≤4}若A∪B=A则BÍA;①、当B =Æ时,由△<0则-1<a<2;②、当B≠Æ时,由
 △≥0
△≥0
¦(1)≥0
¦(4)≥0
对称轴 1≤≤4 Þ2≤a≤ ∴{a|-1<a≤}为所求
★21题:如图,在某水渠同侧有甲、乙两个化工厂,为了保护环境,需将甲、乙两个工厂的污水经过处理之后再排入水渠,为此现设计有两种方案:
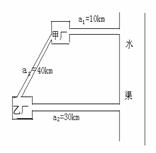 方案一:在甲、乙两厂各建一个污水处理厂,分别处理本厂的污水,然后各自通过新建的管道a1(长10km)、a2(长30km)将污水处理之后再排入水渠;
方案一:在甲、乙两厂各建一个污水处理厂,分别处理本厂的污水,然后各自通过新建的管道a1(长10km)、a2(长30km)将污水处理之后再排入水渠;
方案二:只在甲厂修建一个污水处理厂,乙厂的污水则通过修复甲、乙两厂间的旧管道a3(长40km),然后经此输入污水处理厂,再将两厂的污水经过处理之后,通过新管道a1排入水渠。
已知建立污水处理厂的费用为M=60Q2(万元),辅设新管道的费用为N=6Q·L(万元),其中Q表示污水量(吨/秒),L表示管道长(km),而又已知修复1km旧管道的费用仅是辅设1km新管道费用的25%;
(Ⅰ)、当乙工厂的污水排放量为5吨/秒时,记方案一中的总费用为W万元,记方案二中的总费用为P万元,设甲厂的污水排放量为Q1吨/秒,请写出W与Q1之间的函数关系式,以及P与Q1之间的函数关系式;(Ⅱ)、在总费用不超过4200万元,且乙厂的污水排放量又为5吨/秒的条件下,若甲厂的污水排放量达到了3吨/秒以上,问应选择使用哪种方案,说明理由。
解:①、W=60Q12+6Q1×10+60×52+6×5×30=60Q12+60Q1+2400
②、P=60(Q1+5)+25%×6×5×40+6(Q1+5)×10=60Q12+660Q1+2100
考察方案一:60Q12+60Q1+2400≤4200,则0≤Q1≤5,
考察方案二:60Q12+660Q1+2100≤4200,则0≤Q1≤<3
∴应使用方案一更好一些。
备选例题:
[★题22]已知集合A={ x|x2-5x+4≤0}B={x|x2-2ax+a≤0},若A∪B=A,求a的取值范围
(解、{a|-1≤a≤})
[★题4]已知函数¦(x)=定义域为集合A,函数g(x)=lg[(x-a-1)(2a-x)]定义域为集合B,若BÍA求实数a的取值范围
解、集合A={x|x<-1或 x≥1}
①、当a<1时,B=(2a,a+1),则2a≥1或a+1≤-1; ∴{a|≤a<1或a≤-2}
②、当a=1时,B=Æ 满足要求;③、当a>1时, B=(a+1,2a),则2a≤-1或a+1≥1则a>1
∴a∈[,+∞)∪(-∞,-2]为所求
★[题]、已知洞口县半江水库的最大库容量为128000m3,当山洪暴发时,估计注入水库的水量S(单位:m3)与天数n (n∈N*,N≤10)存在有下列函数关系式:S=5000;现在此水库的存水量已有80000 m3,在山洪暴发到来之时,水库方面将立即开闸放水泄洪,且每天的泄洪量是4000 m3,据此请你进行预测评估,在这10天当中水库的堤坝是否存在危险?若存在危险,说明是第几天或哪几天会发生危险;若不存在危险,请报告理由。
★[题]为保护我国某种特种水泥工业的发展,决定对进口的该种水泥征收附加税。已知此种日本产的水泥在我国的市场零售价为250元/吨时,每年的销售量为40万吨;现在当我国政府对其征收的附加税标准达到t吨/百元时,则每年该种水泥的销售量将减少t万吨,如果我国政府计划在该项经营中,使每年所征收的附加税收入不低于600万元,问该项附加税的税率应控制在哪个范围之内?
21.(本小题满分12分)
A、B两城相距100km,在两地之间距A城xkm处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数 .若A城供电量为20亿度/月,B城为10亿度/月.
.若A城供电量为20亿度/月,B城为10亿度/月.
(Ⅰ)把月供电总费用y表示成x的函数,并求定义域;
(Ⅱ)核电站建在距A城多远,才能使供电费用最小.
解:(Ⅰ)y=5x2+ (100-x)2(10≤x≤90);
(100-x)2(10≤x≤90);
(Ⅱ)由y=5x2+ (100-x)2=
(100-x)2=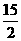 x2-500x+25000=
x2-500x+25000=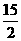
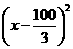 +
+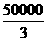 .
.
则当x=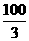 米时,y最小.
米时,y最小.
故当核电站建在距A城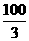 米时,才能使供电费用最小.
米时,才能使供电费用最小.
★11、已知集合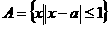 ,
,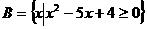 ,若
,若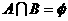 ,则实数
,则实数 的取值范围是
.
的取值范围是
.
★12、A={a²,a+1,-3},B={a-3,2a-1,a²+1},若A∩B={-3},那么a=_______.
★13、设全集I={0,1,2,3,4},集合A={0,1,2,3},集合B={2,3,4},则(C IA)∩(CI B)=__________.
★14、已知不等式5-x>7|x+1|与不等式ax2+bx-2>0的解集相同,则a=__-4__;b=___-9__
★15、设非空集合A={x|2a+1≤x≤3a-5},B={x|3≤x≤22},则能使A A∩B成立的a值的集合为__________。
A∩B成立的a值的集合为__________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com