4、解三角形时，要充分利用正弦定理、余弦定理，结合三角形的内角和定理，三角变形公式去处理问题；

3、三角函数的图象和性质，要注意定义域、值域、奇偶性、图象对称性、周期性、单调性、最值；正、余弦函数作图的“五点法”，以及图象的变换。

2、变形时，要注意角与角之间的相互关系，最常用的有：切割化弦、高次降幂、异角化同角等；(化同名、化同次、化同角)

1、三角变形公式主要是：

①诱导公式；②sin(a±b),cos(a±b),tan(a±b);③sin2a,cos2a,tan2a;③sin²a,cos²a;④asinq+bcosq;

⑤注意常数代换(如1= sin²a+cos²a;=sin30°=cos60°等；角的配凑(如a=(a+b)-b，2a=(a+b)+(a-b)，a=+等)

3、　 向量的加法、减法：平行四边形法则和三角形法则

★　　 例题1、一艘船从A点出发以2km/h的速度向垂直于对岸的方向行驶，同时河水的速为2km/h；求船实际航行的速度大小和方向。(答案：4km/h，方向与水流方向成60°角)

★[※题2]①设O为平面上一定点,A,B,C是平面上不共线的三个点,动点P满足=+l(+),l∈[0,+∞),则点P的轨迹一定通过△ABC的( D　 )

A 外心 　　　B 垂心 　　　C 内心 　　　　D 重心　

②将上题中的条件改为=+l(+)则应选(　 C　 )

★　　 例题3：(1)、化简下列各式：①+；②+-；③++；④(-)+(-)其中结果为0的有①③④

( 2)、在平行四边形ABCD中，=,DB=,则有:=-,=+-

2、　 向量的表示：、、区别于||、||

1、　 向量、平行向量(共线向量)、零向量、单位向量、相等向量：

17．如图，已知：平面α∥平面β，A、C∈α，B、D∈β，AC与BD为异面直线，AC＝6，BD＝8，AB＝CD＝10，AB与CD成60°的角，求AC与BD所成的角．

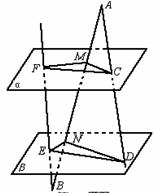
16．如图已知平面α∥平面β，线段AB分别交α、β于M、N，线段AD分别交α、β于C、D，线段BF分别交α，β于F、E，若AM＝m，BN＝n，MN＝P，求△END与△FMC的面积之比．