
题目列表(包括答案和解析)
2、若A(3,-2),B(-9,4),C(x,0)三点共线,则x=( )
A、1 B、-1 C、0 D、7
1、若经过P(-2,m)和Q(m,4)的直线的斜率为1,则m=( )
A、1 B、4 C、1或3 D、1或4
2、两直线垂直的判定:
(1)一条直线的斜率为0,另一条直线的斜率不存在,则这两直线垂直;
(2)如果两条直线 、
、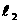 的斜率都存在,且都不为0,则
的斜率都存在,且都不为0,则 ⊥
⊥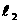 Û k1·k2=-1
Û k1·k2=-1
[例题分析]
例1、△ABC为正三角形,顶点A在x轴上,A在边BC的右侧,∠BAC的平分线在x轴上,
求边AB与AC所在直线的斜率。
例2、若经过点P(1-a,1+a)和Q(3,2a)的直线的倾斜角为钝角,求实数a的取值范围。
例3、已知经过点A(-2,0)和点B(1,3a)的直线 与经过点P(0,-1)和点Q(a,-2a)的直线
与经过点P(0,-1)和点Q(a,-2a)的直线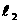 互相垂直,求实数a的值。
互相垂直,求实数a的值。
[课后练习]
1、两直线平行的判定:
(1)两条不重合的直线的倾斜角都是90°,即斜率不存在,则这两直线平行;
(2)两条不重合的直线,若都有斜率,则k1=k2 Û  ∥
∥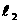
2、直线的斜率
(1)斜率公式:K=tana(a≠90°)
(2)斜率坐标公式:K=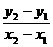 (x1≠x2)
(x1≠x2)
(3)斜率与倾斜角的关系:一条直线必有一个确定的倾斜角,但不一定有斜率。当a=0°时,k=0;当0°<a<90°时,k>0,且a越大,k越大;当a=90°时,k不存在;当90°<a<180°时,k<0,且a越大,k越大。
1、倾斜角的概念:(1)倾斜角:当直线 与x轴相交时,取x轴作为基准,x轴正向与直线
与x轴相交时,取x轴作为基准,x轴正向与直线 向上方向之间所成的角a叫做直线
向上方向之间所成的角a叫做直线 的倾斜角。
的倾斜角。
(2)倾斜角的范围:当 与x轴平行或重合时,规定它的倾斜角a为0°因此0°≤a<180°。
与x轴平行或重合时,规定它的倾斜角a为0°因此0°≤a<180°。
18.解:(1)由框图知 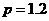 元
元
所以 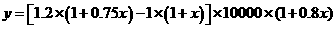
即 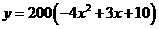
(2)2007年利润为 元
元
令 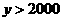 得
得
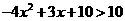

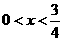
17.解:(1)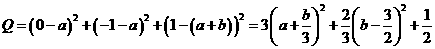
当 时,
时,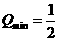 即
即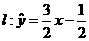
(2)点D在直线上
16.解:(1)A. 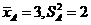 B.
B. 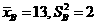
C. D.
D.
(2)规律:如果样本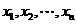 的平均数为
的平均数为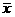 ,方差为
,方差为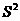 ,则样本
,则样本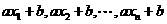 的平均数为
的平均数为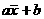 ,方差为
,方差为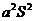
(3)由(2)知,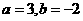 ,所以这组数据的平均数是
,所以这组数据的平均数是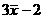 ,方差为
,方差为
15.解:(1)图略
(2)经计算 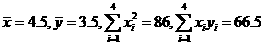

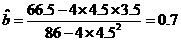
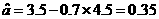

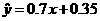
(3)当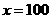 时,
时,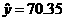 ,降低了标准煤
,降低了标准煤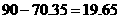 吨
吨
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com