
题目列表(包括答案和解析)
8、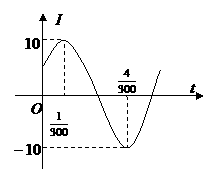 方程:
方程: 的解集是_______________________________________.
的解集是_______________________________________.
7、已知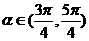 ,
,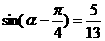 ,则
,则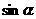 的值为___________________.
的值为___________________.
6、函数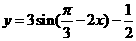 (
(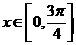 )的单调递增区间是_____________________.
)的单调递增区间是_____________________.
5、函数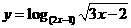 的定义域是______________________.
的定义域是______________________.
4、计算: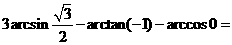 _____________.
_____________.
3、化简: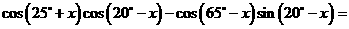 _____________.
_____________.
2、计算: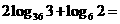 ____________.
____________.
1、若角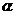 的终边上有一点
的终边上有一点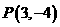 ,则
,则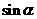 的值是___________________.
的值是___________________.
20.(本题满分16分)
(1)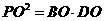 ,DO=1,取AB中点E,连DE,故DE//BC,连PE,故
,DO=1,取AB中点E,连DE,故DE//BC,连PE,故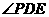 (或其补角)为异面直线PD与BC所成角,
(或其补角)为异面直线PD与BC所成角,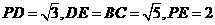 ,
,
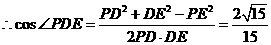 。
。
(2)连OE,PE,可证得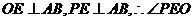 为二面角P-AB-C的平面角,
为二面角P-AB-C的平面角,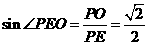 ,
,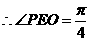 。
。
(3)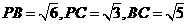 ,
,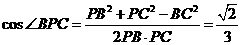 。
。
若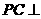 面BMD,则
面BMD,则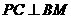 ,
,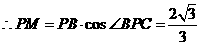 ,
,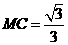 ,
,
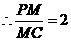 。
。
本题满分16分)如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与
直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°
(Ⅰ)求证:AC⊥BM;
(Ⅱ)求二面角M-AB-C的平面角的正切值;(Ⅲ)求多面体PMABC的体积.
 在正三角形ABC中,E、F分别是AB、
在正三角形ABC中,E、F分别是AB、
AC边上的点,满足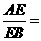
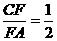 (如图1).
(如图1).
将△AEF沿EF折起到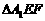 的位置,使二
的位置,使二
面角A1-EF-B成直二面角,连结A1B、A1C.
(如图2)
(1)求证:A1E⊥平面BEC;
(2)求直线A1E与平面A1BC所成角的大小
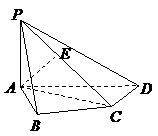
如图,在四棱锥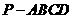 中,
中,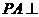 底面
底面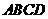 ,
,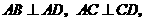
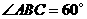 ,
,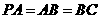 ,
,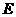 是
是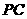 的中点.
的中点.
(Ⅰ)求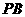 和平面
和平面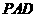 所成的角的大小;
所成的角的大小;
(Ⅱ)证明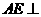 平面
平面 ;
;
(Ⅲ)求二面角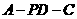 的正弦值..
的正弦值..
(Ⅰ)解:在四棱锥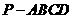 中,因
中,因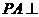 底面
底面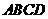 ,
,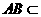 平面
平面 ,故
,故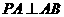 .
.
 又
又 ,
,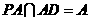 ,从而
,从而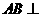 平面
平面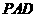 .故
.故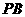 在平面
在平面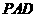 内的射影为
内的射影为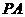 ,从而
,从而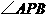 为
为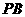 和平面
和平面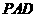 所成的角.
所成的角.
在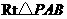 中,
中,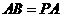 ,故
,故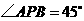 .
.
所以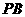 和平面
和平面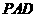 所成的角的大小为
所成的角的大小为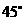 .
.
(Ⅱ)证明:在四棱锥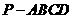 中,
中,
因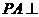 底面
底面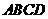 ,
,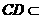 平面
平面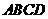 ,故
,故 .
.
由条件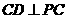 ,
, ,
,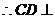 面
面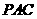 .
.
又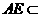 面
面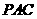 ,
,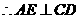 .
.
由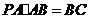 ,
,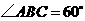 ,可得
,可得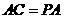 .
.
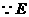 是
是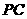 的中点,
的中点,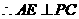 ,
,
 .综上得
.综上得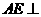 平面
平面 .
.
(Ⅲ)解:过点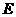 作
作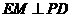 ,垂足为
,垂足为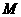 ,连结
,连结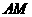 .由(Ⅱ)知,
.由(Ⅱ)知,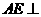 平面
平面 ,
,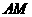 在平面
在平面 内的射影是
内的射影是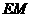 ,则
,则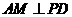 .
.
因此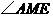 是二面角
是二面角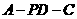 的平面角.
的平面角.
由已知,可得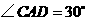 .设
.设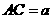 ,可得
,可得
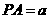 ,
,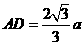 ,
,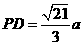 ,
,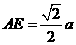 .
.
在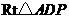 中,
中,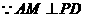 ,
,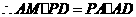 ,则
,则
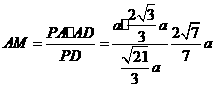 .
.
在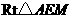 中,
中, .
.
所以二面角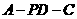 的大小
的大小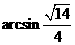 .
.
命题、校对:孟素红
(Ⅰ)∵平面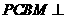 平面
平面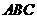 ,
,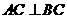 ,
,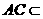 平面
平面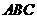 .
.
∴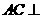 平面
平面
又∵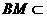 平面
平面
∴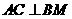
(Ⅱ)取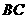 的中点
的中点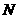 ,则
,则 .连接
.连接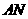 、
、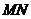 .
.
∵平面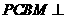 平面
平面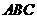 ,平面
,平面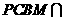 平面
平面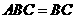 ,
,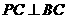 .
.
∴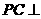 平面
平面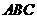 .
.
∵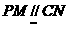 ,∴
,∴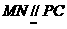 ,从而
,从而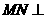 平面
平面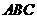 .
.
作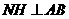 于
于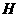 ,连结
,连结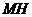 ,则由三垂线定理知
,则由三垂线定理知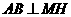 .
.
从而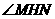 为二面角
为二面角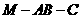 的平面角.
的平面角.
∵直线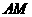 与直线
与直线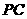 所成的角为60°,
所成的角为60°,
∴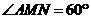 .
.
在 中,由勾股定理得
中,由勾股定理得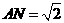 .
.
在 中,
中,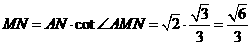 .
.
在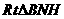 中,
中,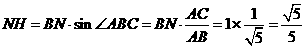 .
.
在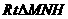 中,
中,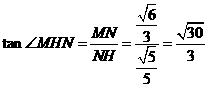
故二面角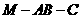 的大小为
的大小为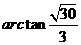
(Ⅱ)如图以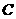 为原点建立空间直角坐标系
为原点建立空间直角坐标系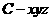 .
.
设
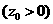 ,
,
有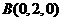 ,
,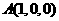 ,
,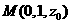 .
.
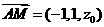 ,
,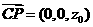
由直线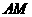 与直线
与直线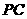 所成的角为60°,得
所成的角为60°,得
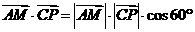
即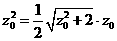 ,解得
,解得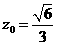 .
.
∴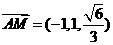 ,
,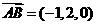
设平面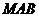 的一个法向量为
的一个法向量为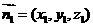 ,则
,则
由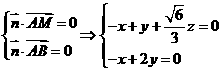 ,取
,取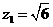 ,得
,得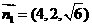
取平面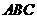 的一个法向量为
的一个法向量为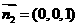
则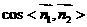
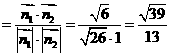
由图知二面角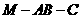 为锐二面角,故二面角
为锐二面角,故二面角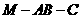 的大小为
的大小为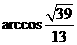 .
.
(Ⅲ)多面体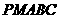 就是四棱锥
就是四棱锥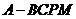
 .
.
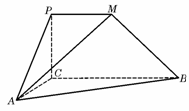
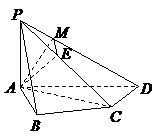
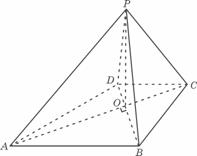
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=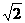 ,PB⊥PD.
,PB⊥PD.
(Ⅰ)求异面直线PD与BC所成角的余弦值;
(Ⅱ)求二面角P-AB-C的大小;
(Ⅲ)设点M在棱PC上,且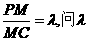 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.
(06全国二)如图,在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点.
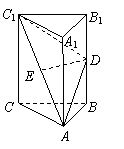 (Ⅰ)证明:ED为异面直线BB1与AC1的公垂线;
(Ⅰ)证明:ED为异面直线BB1与AC1的公垂线;
(Ⅱ)设AA1=AC=AB,求二面角A1-AD-C1的大小.
19.(本题满分16分)
解:(1)依题设,圆 的半径
的半径 等于原点
等于原点 到直线
到直线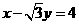 的距离,
的距离,
即 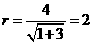 .得圆
.得圆 的方程为
的方程为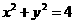 .
.
(2)不妨设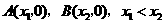 .由
.由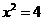 即得
即得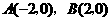 .设
.设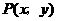 ,由
,由 成等比数列,得
成等比数列,得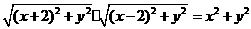 ,即
,即 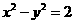 .
.
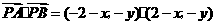
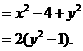
由于点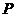 在圆
在圆 内,故
内,故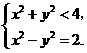 由此得
由此得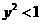 .所以
.所以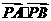 的取值范围为
的取值范围为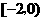 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com