
题目列表(包括答案和解析)
2、下列说法正确的是
A、三点确定一个平面 B、四边形一定是平面图形
C、梯形一定是平面图形
D、平面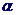 和平面
和平面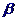 有不同在一条直线上的三个交点
有不同在一条直线上的三个交点
1、线段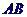 在平面
在平面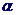 内,则直线
内,则直线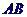 与平面
与平面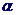 的位置关系是
的位置关系是
A、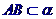 B、
B、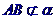 C、由线段
C、由线段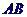 的长短而定 D、以上都不对
的长短而定 D、以上都不对
性质定理:①文字表述 ②数学符号语言:α⊥β a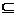 α α∩β=L
a⊥L 即a⊥β
α α∩β=L
a⊥L 即a⊥β
思路:空间做垂线时,找垂足位置的依据--要做垂线,先找垂直平面与交线。垂面可见,垂足可做。
(3)基础演练:
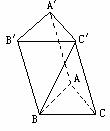
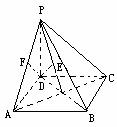 题1:如图:在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥底面ABCD,
且PD=AD=1,则
题1:如图:在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥底面ABCD,
且PD=AD=1,则
(1)直线BC到平面PAD的距离为______1_____(找)
(2)点D到平面PAC的距离为________/3__(做)
(3)点C到平面PAB的距离为______/2____(先转化→再做)
题2:填空:
(1)平面α∥平面β, 平面β⊥平面γ,则平面α与平面γ
的位置关系为_______a⊥γ__
(2) 平面α⊥平面β, 平面β⊥平面γ,则平面α与平面γ的位置关系为____a∥γ或a与γ相交_____.
(3)直线a⊥平面α, 直线a⊥平面β,则平面α与平面β的位置关系为____a∥b_____.
(4)直线a⊥平面α, 直线b⊥平面β,直线a⊥直线b,则平面α与平面β的位置关系___a⊥b.
题3:已知m、n、l为不同的直线,α、β、γ为不同的平面,则真命题序号有__①②④_______
①α⊥γ β∥γ 则α⊥β ②l∥α l⊥β则α⊥β ③m⊥α n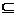 β m⊥n 则α⊥β
β m⊥n 则α⊥β
 ④α∥β m⊥α n∥β
则m⊥n ⑤α⊥β α∩β=m n⊥m 则n⊥β
④α∥β m⊥α n∥β
则m⊥n ⑤α⊥β α∩β=m n⊥m 则n⊥β
⑥β∩γ=l l∥α m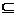 α m⊥γ
则l⊥m m∥β
α m⊥γ
则l⊥m m∥β
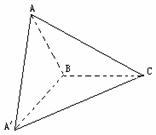
题4:三角形ABC中 AB=BC=1, ∠ABC=120o, 将三角形ABC所在平面沿BC边所在的直线旋转90 o之后,得到平面A′BC ,
(1)求AA′与平面A′BC所成角的大小?
(2)求二面角A-BA′-C的平面角的大小?
(3)求点B到平面AA′C的距离?
 (4)巩固练习:
(4)巩固练习:
题1、斜三棱柱ABC-A′B′C′中∠BAC=90 o, 且B C′⊥AC,过C′
做C′H⊥平面ABC,垂足为H,则( B )
A、点H落于直线AC上 B、点H落于直线AB上
 C、点H落于直线BC上
D、点H落于三角形ABC之内
C、点H落于直线BC上
D、点H落于三角形ABC之内
题2、在四棱锥P-ABCD中,PA⊥底面ABCD,且ABCD为菱形,M在PC边上滑动,则当点
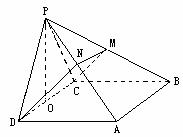 M满足___MB⊥PC______时平面MBD⊥平面PCD。
M满足___MB⊥PC______时平面MBD⊥平面PCD。
题3:四棱锥P-ABCD中,侧面PCD为正△,且与底面ABCD垂直,
已知底面ABCD为菱形,其边长为2,且∠ADC=60 o,M为PB中点。
① 求证:PA⊥CD
② 求PB与底面ABCD所成的角
③ 求证:平面CDM⊥平面PAB。
解: 注意到PA⊥面CDMN
 (5)回味高考:
(5)回味高考:
题1:(湖南05年文科4题)正方体ABCD-A′B′C′D′中棱长为1,E为A′B′中点,则E到平面ABC′D′距离为( B )
A B C D
题2:(湖南05年文科15题)平面α、β和直线m,
给出条件①m∥α
②m⊥α ③m α ④α⊥β ⑤α∥β 则
α ④α⊥β ⑤α∥β 则
(1)当满足条件___③⑤______时有m∥β
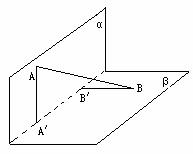 (2)当满足条件____②⑤_____时有m⊥β
(2)当满足条件____②⑤_____时有m⊥β
题3:(06年全国文7题)平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角为45 o、30 o,过A、B分别做两平面交线的垂线,垂足为A′、B′,设AB=12,则A′B′=( B )A、4 B、6 C、8 D、9
归纳总结:(2)求距离的一般方法和步骤是:一作--作出表示距离的线段;二证--证明它就是所要求的距离;三算--计算其值.此外,我们还常用体积法求点到平面的距离.
(3)求距离的关键是化归。即空间距离与角向平面距离与角化归,各种具体方法如下:
①求空间中两点间的距离,一般转化为解直角三角形或斜三角形。
②求点到直线的距离和点到平面的距离,一般转化为求直角三角形斜边上的高;或利用三棱锥的底面与顶点的轮换性转化为三棱锥的高,即用体积法。
高一数学必修2立体几何测试题(自测用)
方法1:判定定理:①文字表述 ②数学符号语言:a α 且a⊥β则α⊥β
α 且a⊥β则α⊥β
→思路:在一个平面之内找出一条直线,证明它垂直于另一个平面
方法2: 求出该二面角的平面角等于90度。 方法3: 向量法:计算出两个平面的法向量·=0
2、几何意义:①直二面角 ②法向量互相垂直的两个平面
1、生活实例:教室中黑板面与地面间关系,打开的手提电脑……
2、举例分析
例1、正方形ABCD的边长是2,E、F分别是AB和CD的中点,将正方形沿EF折成直二面角(如图所示).M为矩形AEFD内一点,如果∠MBE=∠MBC,MB和平面BCFE所成角的正切值为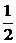 ,那么点M到直线EF的距离为 。
,那么点M到直线EF的距离为 。
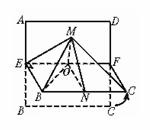
例2.如图,四面体ABCD中,O、E分别BD、BC的中点,CA=CB=CD=BD=2。△ABD为等腰直角三角形。 (Ⅰ)求证:AO⊥平面BCD; (Ⅱ)求异面直线AB与CD所成角的余弦值;
(Ⅲ)求点E到平面ACD的距离。
解:注意平移之后再求距离的问题的应用.
 ★[例题3]、如图,四棱锥
★[例题3]、如图,四棱锥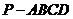 的底面为菱形,且
的底面为菱形,且 ,
,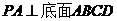 ,
,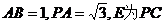 的中点.
的中点.
(1)求直线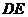 与平面
与平面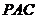 所成角的大小; (2)求二面角
所成角的大小; (2)求二面角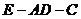 的平面角的正切值; (3)在线段
的平面角的正切值; (3)在线段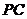 上是否存在一点
上是否存在一点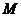 ,使
,使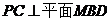 成立?如果存在,求出
成立?如果存在,求出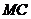 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
解;本题最好使用几何法加以处理.
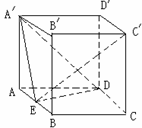 ★[例题4]、如图,直平行六面体ABCD-A′B′C′D′的底面ABCD是边长为2的菱形,∠BAD=60°, E为AB的中点,二面角A′-ED-A为60°;
★[例题4]、如图,直平行六面体ABCD-A′B′C′D′的底面ABCD是边长为2的菱形,∠BAD=60°, E为AB的中点,二面角A′-ED-A为60°;
(1)、求证:平面A′ ED⊥平面ABB′A′;(2)、求二面角A′-ED-C′ 的大小;
(3)、求点C′ 到平面A′ED的距离。
解:本题第一问最好用几何法处理,第二问要注意到A′E⊥ED且C′D⊥ED,再用向量法处理;第三问则最好用向量法去处理.
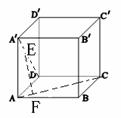
[例题5]如图,在正方体ABCD-A′B′C′D′中,EF是异面直线AC与A′D的公垂线,则由正方体的八个顶点所连接的直线中,与EF平行的直线( A )
A 有且只有一条 B 有二条 C 有四条 D 不存在
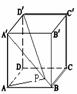 ★[例题6]如图所示,在单位正方体ABCD-A′B′C′D′中,若四边形A′ABB′的对角线A′B上存在一点P使得AP+D′P最小,则AP+D′P的最小值是_____
★[例题6]如图所示,在单位正方体ABCD-A′B′C′D′中,若四边形A′ABB′的对角线A′B上存在一点P使得AP+D′P最小,则AP+D′P的最小值是_____
解:考虑图形的翻折去处理.
1.基本知识: (1)空间中的距离是立体几何的重要内容,其内容主要包括:点点距,点线距,点面距,线线距,线面距,面面距。其中重点是点点距、点线距、点面距以及两异面直线间的距离.因此,掌握点、线、面之间距离的概念,理解距离的垂直性和最近性,理解距离都指相应线段的长度,懂得几种距离之间的转化关系,所有这些都是十分重要的。
(2)求距离的重点在点到平面的距离,直线到平面的距离和两个平面的距离可以转化成点到平面的距离,一个点到平面的距离也可以转化成另外一个点到这个平面的距离。
(3)点到平面的距离
平面外一点P 在该平面上的射影为P′,则线段PP′的长度就是点到平面的距离;
求法:1“一找二证三求”,三步都必须要清楚地写出来。 2等体积法。
(4)直线与平面的距离:一条直线和一个平面平行,这条直线上任意一点到平面的距离,叫做这条直线和平面的距离;
(5)平行平面间的距离:两个平行平面的公垂线段的长度,叫做两个平行平面的距离。
求距离的一般方法和步骤:应用各种距离之间的转化关系和“平行移动”的思想方法,把所求的距离转化为点点距、点线距或点面距求之,其一般步骤是:
 ①找出或作出表示有关距离的线段; ②证明它符合定义; ③归到解某个三角形.若表示距离的线段不容易找出或作出,可用体积等积法计算求之。
①找出或作出表示有关距离的线段; ②证明它符合定义; ③归到解某个三角形.若表示距离的线段不容易找出或作出,可用体积等积法计算求之。
3.掌握平行平面间的距离,会求二面角及其平面角;
1.掌握两条直线所成的角和距离的概念及等角定理;(对于异面直线的距离,只要求会计算已给出公垂线时的距离)。 2.掌握点、直线到平面的距离,直线和平面所成的角;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com