
题目列表(包括答案和解析)
(17)计算下列各式
(Ⅰ)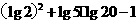
(Ⅱ) 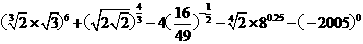
(18)定义在实数R上的函数y= f(x)是偶函数,当x≥0时,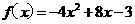 .
.
(Ⅰ)求f(x)在R上的表达式;
(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明).
(19)已知二次函数f(x)图象过点(0,3),它的图象的对称轴为x = 2,
且f(x)的两个零点的平方和为10,求f(x)的解析式.
(20) 已知函数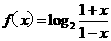 ,(x∈(- 1,1).
,(x∈(- 1,1).
(Ⅰ)判断f(x)的奇偶性,并证明;
(Ⅱ)判断f(x)在(- 1,1)上的单调性,并证明.
(21) 商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少。把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的相同价格(标价)出售. 问:
(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
(13)函数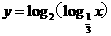 的定义域为 .
的定义域为 .
(14)若集合M={x| x2+x-6=0},N={x| kx+1=0},且N M,则k的可能值组成的集合为
.
M,则k的可能值组成的集合为
.
(15)设函数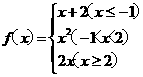 ,若f(x)=3,则x= .
,若f(x)=3,则x= .
(16)有以下4个命题:
①函数f(x)= ax(a>0且a≠1)与函数g(x)=log aax(a>0且a≠1)的定义域相同;
②函数f(x)=x3与函数g(x)=3 x的值域相同;
③函数f(x)=(x-1)2与g(x)=2 x -1在(0,+∞)上都是增函数;
④如果函数f(x)有反函数f -1(x),则f(x+1)的反函数是f -1(x+1).
其中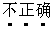 的题号为
.
的题号为
.
(1)若集合A={1,3,x},B={1,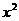 },A∪B={1,3,x},则满足条件的实数x的个数有( )
},A∪B={1,3,x},则满足条件的实数x的个数有( )
(A) 1个 (B) 2个 (C)3个 (D) 4个
(2)集合M={(x,y)| x>0,y>0},N={(x,y)| x+y>0,xy>0}则( )
(A)M=N (B)M  N (C)M
N (C)M  N (D)M
N (D)M N=
N=
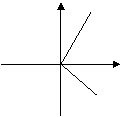
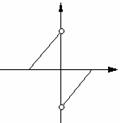
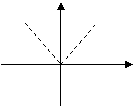
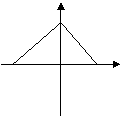 (3)下列图象中不能表示函数的图象的是 ( )
(3)下列图象中不能表示函数的图象的是 ( )
 y
y
y
y
y
y
o x x o x o x
(A) (B) (C) (D)
(4)若函数y=f(x)的定义域是[2,4],则y=f(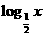 )的定义域是( )
)的定义域是( )
(A) [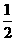 ,1] (B) [4,16] (C)[
,1] (B) [4,16] (C)[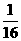 ,
,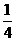 ] (D)[2,4 ]
] (D)[2,4 ]
(5)函数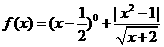 的定义域为( )
的定义域为( )
(A)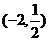 (B)(-2,+∞)
(C)
(B)(-2,+∞)
(C)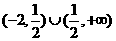 (D)
(D)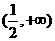
(6)设偶函数f(x)的定义域为R,当 时f(x)是增函数,则
时f(x)是增函数,则 的大小关系是( )
的大小关系是( )
(A)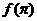 >
>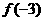 >
>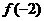 (B)
(B)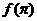 >
>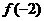 >
>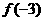
(C)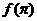 <
<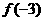 <
<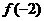 (D)
(D)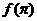 <
<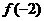 <
<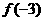
(7)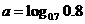 ,
,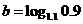 ,
,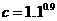 ,那么( )
,那么( )
(A)a<b<c (B)a<c<b (C)b<a<c (D)c<a<b
(8)已知函数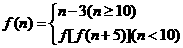 ,其中n
,其中n N,则f(8)=( )
N,则f(8)=( )
(A)6 (B)7 (C) 2 (D)4
(9)某工厂今年前五个月每月生产某种产品的数量C(件)关于时间t(月)的函数图象如图所示,则这个工厂对这种产品来说( )
C
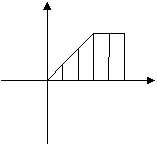
O 一二 三 四五 t
(A)一至三月每月生产数量逐月增加,四、五两月每月生产数量逐月减少
(B)一至三月每月生产数量逐月增加,四、五月每月生产数量与三月持平
(C)一至三月每月生产数量逐月增加,四、五两月均停止生产
(D)一至三月每月生产数量不变,四、五两月均停止生产
(10)若函数f(x)和g(x)都为奇函数,函数F(x)=af(x)+bg(x)+3在(0,+∞)上有最大值10,则F(x)在(-∞,0)上有( )
(A) 最小值 -10 (B)最小值 -7 (C)最小值 -4 (D)最大值 -10
(11)若函数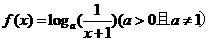 的定义域和值域都是[0,1],则a=( )
的定义域和值域都是[0,1],则a=( )
(A)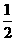 (B)
(B)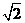 (C)
(C)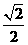 (D)2
(D)2
(12)如果二次函数f(x)=3x2+bx+1在(-∞,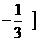 上是减函数,在
上是减函数,在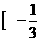 ,+∞)上是增函数,则f(x)的最小值为( )
,+∞)上是增函数,则f(x)的最小值为( )
(A)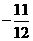 (B)
(B)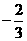 (C)
(C) (D)
(D)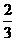
21,已知点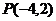 和直线l:
和直线l: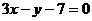
求:(1)过点P与直线l平行的直线方程一般式;
(2)过点P与直线l垂直的直线方程一般式;
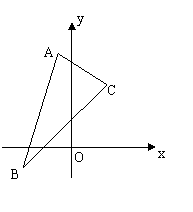
22,已知 三个顶点是
三个顶点是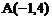 ,
,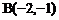 ,
,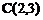 .
.
(Ⅰ)求BC边中线AD所在直线方程;
(Ⅱ)求点A到BC边的距离.
23,求经过点A(0,4),B(4,6)且圆心在直线x―2y―2=0上的圆的方程;
24,已知直线:y=x+b和圆x2+y2+2x―2y+1=0(1)若直线和圆相切,求直线的方程;(2)若b=1,求直线和圆相交的弦长;
25,在四棱锥P―ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,
侧棱PA与底面成450的角,M,N,分别是AB,PC,的中点;
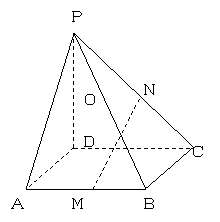 (1)求证:MN∥平面PAD;(2)求四棱锥P-ABCD的体积.
(1)求证:MN∥平面PAD;(2)求四棱锥P-ABCD的体积.
26,已知方程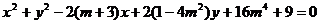 表示一个圆,
表示一个圆,
(1)求实数m的取值范围;(2)求该圆半径r的取值范围;(3)求圆心的轨迹方程;
16,点A(1,3)关于点P(2,5)对称点A'的坐标是
17,已知A(-3,-5),B(5,1),则以线段AB为直径的圆的方程一般式为_______
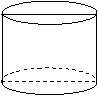
 18,如下左图是一个底面直径和高都是4的圆柱的侧面积为 _____(最后的结果保留π)
18,如下左图是一个底面直径和高都是4的圆柱的侧面积为 _____(最后的结果保留π)
19,光线从点(―1,3)射向x轴,经过x轴反射后过点(4,6),则反射光线所在的直线方程一般式是
20,已知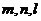 是直线,
是直线,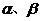 是平面,下列命题中:
是平面,下列命题中:
①若 垂直于
垂直于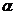 内两条直线,则
内两条直线,则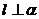 ;②若
;②若 平行于
平行于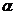 ,则
,则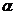 内可有无数条直线与
内可有无数条直线与 平行;
平行;
③若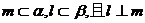 ,则
,则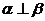 ;④若m⊥n,n⊥l则m∥l;
;④若m⊥n,n⊥l则m∥l;
⑤若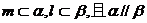 ,则
,则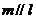 ;正确的命题个数为____________。
;正确的命题个数为____________。
19.甲盒中有一个红色球,两个白色球,这3个球除颜色外完全相同,有放回地连续抽取2个,每次从中任意地取出1个球,用列表的方法列出所有可能结果,计算下列事件的概率。
(1)取出的2个球都是白球; (2)取出的2个球中至少有1个白球。
18.已知 ,设计算法流程图,输出
,设计算法流程图,输出 。
。
17.设计算法流程图,要求输入自变量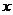 的值,输出函数
的值,输出函数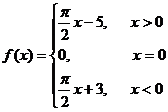 的值,并用复合if语句描述算法。
的值,并用复合if语句描述算法。
16.有一个容量为100的样本,数据的分组及各组的频数如下: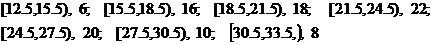 (1)列出样本的频率分布表;(2)画出频率分布直方图和频率折线图。
(1)列出样本的频率分布表;(2)画出频率分布直方图和频率折线图。
15.某小组有三名女生,两名男生,现从这个小组中任意选出一名组长,则其中一名女生小丽当选为组长的概率是___________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com