
题目列表(包括答案和解析)
8.假设一部机器在一天内随机发生一次故障,那么在晚上8点到11点内出故障的概率是( )
A、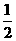 B、
B、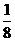 C、
C、 D、
D、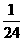
7.函数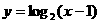 的反函数的图象是( )
的反函数的图象是( )
A.


 B.
C.
D.
B.
C.
D.
|
6.设偶函数f(x)的定义域为R,当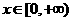 时f(x)是增函数,则
时f(x)是增函数,则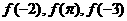 的大小关系是( ) (A)
的大小关系是( ) (A)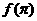 >
>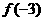 >
>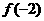 (B)
(B)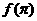 >
>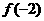 >
>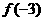
(C)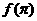 <
<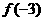 <
<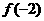 (D)
(D)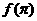 <
<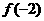 <
<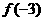
5.已知两直线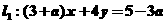 与
与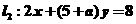 互相 平行,则
互相 平行,则 等于( )
等于( )
A. 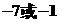 B.
B.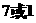 C.
C.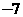 D.
D.
4.若图中直线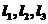 的斜率分别为k1,k2,k3,则有(
)
的斜率分别为k1,k2,k3,则有(
)
A. k2<k1<k3 B.k3<k2<k1 C. k2<k3<k1 D. k1<k3<k2
3.下列命题中,错误的个数有( )个
①.平行于同一条直线的两个平面平行. ②.平行于同一个平面的两个平面平行.
 ③.一个平面与两个平行平面相交,交线平行. ④.一条直线与两个平行平面中的一个相交,则必与另一个平面相交.
③.一个平面与两个平行平面相交,交线平行. ④.一条直线与两个平行平面中的一个相交,则必与另一个平面相交.
A 0个 B 1个 C 2个 D 3个
2. 函数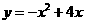 ,
, 的递增区间是( )
的递增区间是( )
A. 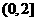 B.
B.
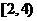 C.
C.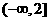 D.
D. 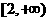
1. 函数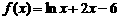 (
( 是以
是以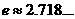 为底的对数)的零点落在区间( )
为底的对数)的零点落在区间( )
A.(2,2.25) B.(2.25,2.5) C.(2.5,2.75) D.(2.75,3)
(17)解:(Ⅰ)原式=lg22+(1- lg2)(1+lg2)-1
=lg22+1- lg22- 1=0
(Ⅱ)原式=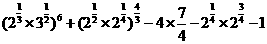
=22×33+2 - 7- 2- 1 =100
(18)解:(Ⅰ)设x<0,则- x>0, 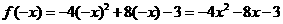 ∵f(x)是偶函数,
∵f(x)是偶函数,
∴f(-x)=f(x) ∴x<0时, 
所以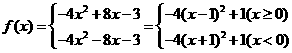
(Ⅱ)y=f(x)开口向下,所以y=f(x)有最大值f(1)=f(-1)=1
函数y=f(x)的单调递增区间是(-∞,-1 和[0,1]
和[0,1]
单调递减区间是 [-1,0]和[1,+∞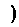
(19)解:设f(x)= ax2+bx+c (a≠0)
因为f(x)图象过点(0,3),所以c =3
又f(x)对称轴为x=2, ∴ 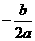 =2即b= - 4a
=2即b= - 4a
所以
设方程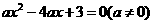 的两个实根为 x1,x2,
的两个实根为 x1,x2,
则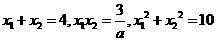
∴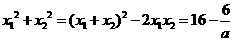 ,所以
,所以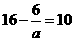
得a=1,b= - 4
所以
(20)证明:(Ⅰ)
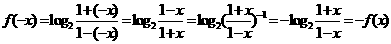
又x∈(-1,1),所以函数f(x)是奇函数
(Ⅱ)设 -1<x<1,△x=x2- x1>0
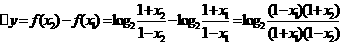
因为1- x1>1- x2>0;1+x2>1+x1>0
所以
所以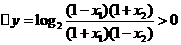
所以函数 在(- 1,1)上是增函数
在(- 1,1)上是增函数
(21)(Ⅰ)设购买人数为n人,羊毛衫的标价为每件x元,利润为y元,
则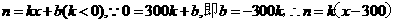
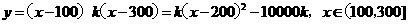
∵k<0,∴x=200时,ymax= - 10000k,
即商场要获取最大利润,羊毛衫的标价应定为每件200元.
(Ⅱ)由题意得,k(x- 100)(x- 300)= - 10000k·75%

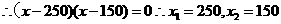
所以,商场要获取最大利润的75%,每件标价为250元或150元.
(13) (0,1)
(14){0,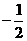 ,
,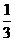 }
}
(15)  (16)
②③④
(16)
②③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com