
题目列表(包括答案和解析)
1.根式的概念:若n>1且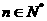 ,则
,则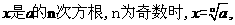
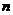 为偶数时,
为偶数时, ;
;
3.计算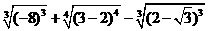
类比平方根、立方根的概念,归纳出n次方根的概念.
n次方根:一般地,若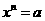 ,则x叫做a的n次方根(throot),其中n >1,且n∈N*,当n为偶数时,a的n次方根中,正数用
,则x叫做a的n次方根(throot),其中n >1,且n∈N*,当n为偶数时,a的n次方根中,正数用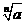 表示,如果是负数,用
表示,如果是负数,用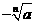 表示,
表示,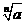 叫做根式.n为奇数时,a的n次方根用符号
叫做根式.n为奇数时,a的n次方根用符号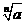 表示,其中n称为根指数,a为被开方数.
表示,其中n称为根指数,a为被开方数.
类比平方根、立方根,猜想:当n为偶数时,一个数的n次方根有多少个?当n为奇数时呢?
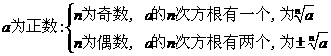
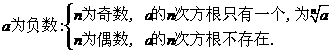
零的n次方根为零,记为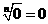
举例:16的次方根为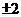 ,
,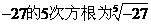 等等,而
等等,而 的4次方根不存在.
的4次方根不存在.
小结:一个数到底有没有n次方根,我们一定先考虑被开方数到底是正数还是负数,还要分清n为奇数和偶数两种情况.
根据n次方根的意义,可得:
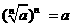
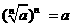 肯定成立,
肯定成立,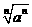 表示an的n次方根,等式
表示an的n次方根,等式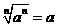 一定成立吗?如果不一定成立,那么
一定成立吗?如果不一定成立,那么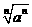 等于什么?
等于什么?
让学生注意讨论,n为奇偶数和a的符号,充分让学生分组讨论.
通过探究得到:n为奇数,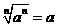
n为偶数, 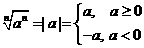
如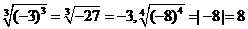
小结:当n为偶数时,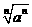 化简得到结果先取绝对值,再在绝对值算具体的值,这样就避免出现错误:
化简得到结果先取绝对值,再在绝对值算具体的值,这样就避免出现错误:
例题:求下列各式的值
(1)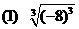
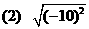
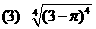
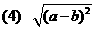
分析:当n为偶数时,应先写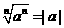 ,然后再去绝对值.
,然后再去绝对值.
思考: 是否成立,举例说明.
是否成立,举例说明.
课堂练习:1. 求出下列各式的值

2.若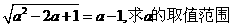 .
.
什么是平方根?什么是立方根?一个数的平方根有几个,立方根呢?
归纳:在初中的时候我们已经知道:若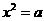 ,则
,则 叫做a的平方根.同理,若
叫做a的平方根.同理,若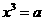 ,则
,则 叫做a的立方根.
叫做a的立方根.
根据平方根、立方根的定义,正实数的平方根有两个,它们互为相反数,如4的平方根为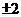 ,负数没有平方根,一个数的立方根只有一个,如―8的立方根为―2;零的平方根、立方根均为零.
,负数没有平方根,一个数的立方根只有一个,如―8的立方根为―2;零的平方根、立方根均为零.
第一课时
2.教具:多媒体
1.学法:讲授法、讨论法、类比分析法及发现法
2.教学难点:分数指数幂及根式概念的理解
1.教学重点:(1)分数指数幂和根式概念的理解;
(2)掌握并运用分数指数幂的运算性质;
3.情态与价值
(1)培养学生观察分析,抽象的能力,渗透“转化”的数学思想;
(2)通过运算训练,养成学生严谨治学,一丝不苟的学习习惯;
(3)让学生体验数学的简洁美和统一美.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com